(02)
NUOVO CONCETTO DI ENTROPIA

INTRODUZIONE

  1. MACCHINE TERMICHE, che eseguono CICLI CHIUSI per trasformare CALORE (Q) in LAVORO.
  2. RENDIMENTO η=L/Q<1, definito dal rapporto fra LAVORO ottenuto (L) e CALORE speso (Q).
  3. Ciclo di CARNOT Invertibile, col massimo RENDIMENTO minore di UNO (η=L/Q<1).

Questi Concetti consentono di definire il Postulato di CARNOT-CLAUSIUS, chiamato SECONDO PRINCIPIO della TERMODINAMICA, che significa: IL CALORE NON PASSA SPONTANEAMENTE DA CORPI CALDI A CORPI FREDDI.

Lo stesso POSTULATO definisce anche l'ENTROPIA dS=δQ/T, una particolare FUNZIONE di STATO che dovrebbe ESPRIMERE la CERTEZZA MATEMATICA della Sua ESISTENZA.

Peraltro non è possibile costruire un MOTORE funzionante con un Ciclo INVERTIBILE (compreso quello di CARNOT) nemmeno ELIMINANDO gli ATTRITI, a causa della CATENA CINEMATICA (link 08,12) che dal CILINDRO all'ALBERO condiziona la sua FORMA geometrica e il RENDIMENTO.

Inoltre, in alternativa al Ciclo di CARNOT, si possono costruire Cicli TERMICI con RENDIMENTO UNITARIO (η=L/Q=1), in particolare i Cicli ENTROPICI (link 07,11) ottenuti come Varianti del Ciclo RANKINE-HIRN, tenendo conto (Link 06,07,10) che il suo PRIMO LATO non si trova (come si crede) nella ZONA LIQUIDA ma sulla prima CURVA Iso-Titolo (dx=0) del FLUIDO.

DEFINIZIONE

L’ENTROPIA dS=δQ/T di un CORPO MATERIALE (M) è una GRANDEZZA Termodinamica (ΔS) definita dal rapporto (ΔS=δQ/T) fra lo SCAMBIO istantaneo di CALORE (δQ≠0) ricevuto o ceduto da M e la TEMPERATURA ASSOLUTA (T) posseduta dal Corpo (M) nello stesso istante, come risulta (⇒) dall’INTEGRALE di CARNOT ∮(δQ/T) esteso ad un CICLO CHIUSO INVERTIBILE:

∮(δQ/T) ⇒ dS=δQ/T

Il SIMBOLO matematico DIREZIONALE (⇒da sinistra a destra) indica il VERSO (irreversibile) della CORRISPONDENZA. Infatti, l’Integrale ∮(δQ/T) a sinistra rappresenta l’IPOTESI fondata sulla reale ESISTENZA dei Cicli REVERSIBILI in particolare quello di CARNOT (link 08,12).

Come dimostreremo in seguito, il DIFFERENZIALE dS=δQ/T (a destra) costituisce l’effettiva Definizione dell’ENTROPIA (ΔS), una FUNZIONE di STATO che non necessita di IPOTESI per confermare la CERTEZZA matematica delle sua ESISTENZA, soprattutto l'INDIPENDENZA dall’INTEGRALE di CARNOT-CLAUSIUS e dal SECONDO PRINCIPIO della TERMODINAMICA.

Malgrado la (relativa) semplicità della definizione in termini infinitesimi (dS=δQ/T), al CONCETTO di ENTROPIA in termini finiti ΔS=∫dS=∫(δQ/T) si attribuiscono SIGNIFICATI notevolmente complessi, a volte INCOMPATIBILI con quella definizione, come: la IRREVERSIBILITA' dei fenomeni reali, la PROBABILITA' degli eventi, la FRECCIA del tempo e tanti ALTRI, in particolare nel Campo della BIOLOGIA, ma soprattutto (il più importante) quello di rappresentare l'UNICA espressione matematica del SECONDO PRINCIPIO della TERMODINAMICA, che senza il supporto dell'ENTROPIA (ΔS) si limiterebbe ad ENUNCIARE l’originario POSTULATO di CLAUSIUS. Il Concetto di ENTROPIA viene ridefinito e applicato da Riviste specializzate, anche in ambito non Termodinamico, a volte con IPOTESI correttive non sempre convincenti, come ad esempio la Enciclopedia Treccani.

ENTROPIA nell’Enciclopedia Treccani

  1. Grandezza che interviene nello studio fisico-chimico delle trasformazioni di un sistema materiale e che dipende unicamente dallo stato del sistema.
  2. In termini matematici si può dire che è funzione delle sole variabili prescelte a caratterizzare tale stato.
  3. La dipendenza è diversa a seconda della natura del sistema (gas perfetto, gas reale, liquido ecc.).
  4. Come risulta dalla meccanica statistica, è la misura del grado di disordine molecolare del sistema ovvero del grado di indeterminazione con il quale si conoscono posizioni e velocità molecolari del sistema.
  5. Come misura del grado di disordine o di indeterminazione di un sistema, è stata utilizzata in campi di applicazione lontani dalla fisica, primo tra tutti la teoria dell’informazione.

RISPONDO: I punti 1) e 2) concordano con la corrispondenza di CLAUSIUS ∮(δQ/T)=0 ⇒ dS=δQ/T (⇒ da sinistra a desta) ma non con quella INVERSA (⇐ da destra a sinistra), venendo così a mancare la RECIPROCITA' (⇔) che dovrebbe essere imposta anche dalla Funzione di Stato chiamata ENTROPIA, mettendo in DUBBIO il presunto LEGAME di quella corrispondenza. Queste (e altre) forme di incompatibilità sono state ELIMINATE dal punto 3): un opportuno e comodo RIMEDIO poco convincente che (come vedremo) non trova conferma nella dimostrazione matematica del CONCETTO di ENTROPIA. Infine, i restanti punti 4) e 5) rappresentano arbitrarie IPOTESI NON DIMOSTRABILI, introdotte allo scopo di SEMPLIFICARE la conoscenza di GRANDEZZE infinitesime non facilmente VALUTABILI.

POSSIBILI CONSEGUENZE

L’EQUAZIONE dS=δQ/T lega i due IFINITESIMI (dS),(δQ) Variabili tendenti a ZERO (→0) ma con modalità generalmente DIFFERENTI (dS→0)<=>(δQ→0), come risulta dalle INTEGRAZIONI ∫dS<=>∫gδQ in Termini Finiti.

Peraltro soltanto l’ENTROPIA (S) è certamente un DIFFERENZIALE (dS) che nel caso dei FLUIDI dipende soltanto da una coppia (x,y) di VARIABILI indipendenti, dS=X(x,y)dx+Y(x,y)dy, e quindi (in linea di principio) il suo INTEGRALE (ΔS=∫dS) si può esprimere (in termini finiti) con EQUAZIONI del tipo ΔS=f(x,y), come in effetti avviene con tutte le altre FUNZIONI di STATO (Pressione, Volume, Temperatura, Entalpia, ecc.).

Invece lo SCAMBIO TERMICO δQ≠0 si risolve sempre (in termini finiti) con INTEGRALI CURVILINEI del tipo Qg=∫gTdS, che dipendono dalla CURVA di INTEGRAZIONE (g) e dai PUNTI ESTREMI (P1,P2)∈(g).

 Insomma QUALCOSA NON CONVINCE, malgrado la presenza del FATTORE INTEGRANTE 1/T che dovrebbe condizionare il significato fisico dell’INFINITESIMO δQ, mentre nella definizione di ENTROPIA dS=δQ/T esiste una Corrispondenza (dS=δQ/T)⇔(δQ=TdS) fra il Differenziale ENTROPICO dS e particolari SCAMBI TERMICI δQ≠0, che in questi casi diventano anch’Essi DIFFERENZIALI ESATTI (δQ=dQ=TdS), come nelle ISOBARICHE (dp=0) e/o nelle ISOCORE (dv=0) dove δQ equivale alla ENTALPIA (δQ)p=(dH)p e alla ENERGIA-INTERNA (δQ)v=(dU)v.

Resta da vedere se esiste effettivamente uno SCAMBIO di CALORE Qg=∫gTdS indipendente dall’ENTROPIA ΔS=∫(δQ/T. A tale scopo conviene (in qualche modo) tentare di SEPARARE i due INFINITESIMI (dS),(δQ), magari cercando di INTEGRARE il DIFFERENZIALE dS=δQ/T con EQUAZIONI Matematiche del Tipo ΔS=∫(δQ/T)=f(x,y).

Un PROBLEMA che vale la pena affrontare, pur sapendo che una sua eventuale SOLUZIONE metterebbe in discussione il SECONDO PRINCIPIO della TERMODINAMICA, da molti accettato senza eccezioni e perciò ritenuto INTOCCABILE, malgrado la sua origine prettamente SPERIMENTALE (Postulato di Carnot-Clausius).

Nuovo CONCETTO di ENTROPIA

1) ENTROPIA dei FLUIDI (LIQUIDI, GAS, MISCUGLI)

La REGOLA delle FASI N=Nm+2-Nf (di GIBBS) esprime il numero dei GRADI di LIBERTA’ (N) di un SISTEMA Materiale, che dipende dal numero (Nm) delle SPECIE CHIMICHE (es. H2O+CO2+…) e dal numero (Nf) delle FASI (Liquidi e/o Vapori).

 Ma nei FLUIDI occorre tener conto del numero dei MISCUGLI Mn=(M1+M2+..) formati da LIQUIDI (M’)n e VAPORI (M”)n definiti dai rispettivi TITOLI xn=(M”/M)n. Quindi nei FLUIDI la REGOLA delle FASI dovrebbe assumere la seguente ESPRESSIONE (1), dove nel nostro caso risulta Nm=1 (es. H2O), Nf=2 (un Liquido M’ col suo Vapore M”), Mn=1 (un solo Miscuglio) ottenendo ancora N=(Nm+2-Nf+Mn)=2 VARIABILI Indipendenti, ad esempio la COPPIA (Pressione, Volume)=(p,v) che definisce il DIFFERENZIALE dT (2) della TEMPERATURA:

(01)

  N=Nm+2-Nf+Mn

Sostituendo Cv,Cp e il DIFFERENZIALE (2), si ottiene il nuovo Infinitesimo (3), nei tre Piani (Pressione,Volume)=(p,v), (Temperatura,Volume)=(T,v) e (Temperatura, Pressione)=(T,p):

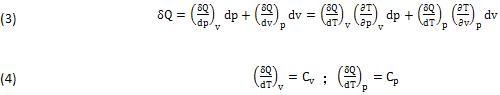
Sostituendo Cv,Cp e il DIFFERENZIALE (2), si ottiene il nuovo Infinitesimo (3), nei tre Piani (Pressione,Volume)=(p,v), (Temperatura,Volume)=(T,v) e (Temperatura, Pressione)=(T,p):

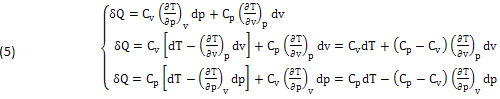
Dividendo membro a membro queste EQUAZIONI per la Temperatura (T), l’ENTROPIA di CARNOT CLAUSIUS (dS=δQ/T) può essere DEFINITA negli stessi PIANI (p,v),(T,v),(T,p).

La NOVITA’ consiste nella SEPARAZIONE dei due INFINITESIMI (dS),(δQ), che risultano generalmente INDIPENDENTI e quindi possono essere DEFINITI SEPARATAMENTE:

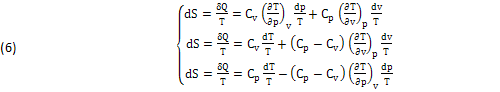
Ma mentre l’ENTROPIA (dS=δQ/T) è certamente un DIFFERENZIALE (Teoremi di CARNOT CLAUSIUS), resta da determinare la vera NATURA ANALITICA dell’altro INFINITESIMO “δQ”, che in certi CASI anch’ESSO può diventare un DIFFERENZIALE (δQ=dQ) come in effetti ACCADE nelle seguenti equazioni (7) che definiscono i due DIFFERENZIALI dell’ENERGIA INTERNA (dU) e della ENTALPIA (dH), dove tutti i TERMINI devono essere necessariamente OMOGENEI:

Tutto questo a titolo PROVVISORIO fino a quando (in alternativa) non si riesca a inventare FLUIDI FRIGORIFERI più convenienti, con TEMPERATURE di Congelamento molto BASSE, per ottenere in ogni luogo LAVORO a spese di un’ UNICA SORGENTE come l’ AMBIENTE CIRCOSTANTE, che significa MOTO PERPETUO di SECONDA SPECIE.

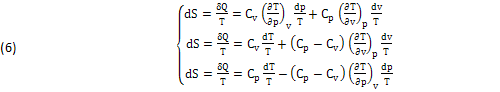
Ma mentre l’ENTROPIA (dS=δQ/T) è certamente un DIFFERENZIALE (Teoremi di CARNOT CLAUSIUS), resta da determinare la vera NATURA ANALITICA dell’altro INFINITESIMO “δQ”, che in certi CASI anch’ESSO può diventare un DIFFERENZIALE (δQ=dQ) come in effetti ACCADE nelle seguenti equazioni (7) che definiscono i due DIFFERENZIALI dell’ENERGIA INTERNA (dU) e della ENTALPIA (dH), dove tutti i TERMINI devono essere necessariamente OMOGENEI:

Questo PROBLEMA può risolversi INTEGRANDO i due SISTEMI (5),(6) in TERMINI FINITI, procedimento laborioso ricordando che in questi CASI,assieme al FLUIDO occorre ASSEGNARE i due Calori Specifici (Cv,Cp). Per semplificare i CALCOLI conviene quindi limitare la RICERCA nel CAMPO dei FLUIDI IDEALI.

2) ENTROPIA dei GAS IDEALI

Per ogni FLUIDO I due CALORI-SPECIFICI Cv,Cp sono FUNZIONI-di-STATO, che diventano COSTANTI nei GAS IDEALI come dimostrano le seguenti Equazioni Sperimentali, dove “R” tiene conto del particolare GAS impiegato e “k” dei GRADI di LIBERTA’ molecolari, con buona approssimazione VALIDI anche per i GAS REALI ad alta TEMPERAURA (T>>TC):

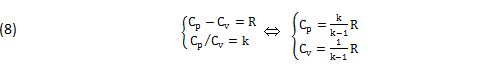
E’ nota anche l’Equazione di Stato, ottenuta dalla Teoria Cinetica e per via Sperimentale:

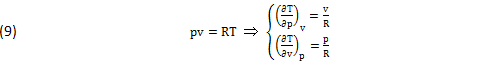
Con opportune CORREZIONI delle due Costanti Fisiche (k,R), queste EQUAZIONI (8),(9) possono estendersi a tutti i GAS REALI e ai MISCUGLI LIQUIDO VAPORE delle MACCHINE TERMICH

In questi casi lo SCAMBIO TERMICO (5) e l’ENTROPIA (6) assumono le forme INFINITESIME (10),(11) facilmente INTEGRABILI lungo ogni trasformazione f(p,v)=0 di "δQ" ma senza alcun vincolo per "dS", diventando DIFFERENZIALI ESATTI (ΔQ,ΔS) con le successive (12),(13):

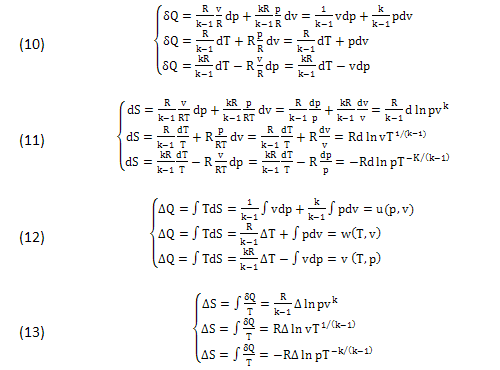
In questi casi l’INFINITESIMO δQ=TdS risulta COMPATIBILE con l'ENTROPIA dS=δQ/T e i DIFFERENZIALI (7):

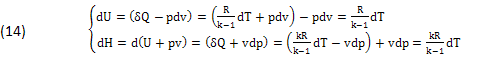
CONCLUSIONE

Si suppone che l’ENTROPIA "S" definita dai TEOREMI di CARNOT-CLAUSIUS rappresenti l’OMONIMO POSTULATO, cioè il SECONDO PRINCIPIO della TERMODINAMICA.

In effetti costituisce un insolito DIFFERENZIALE dS=δQ/T stranamente legato dal FATTORE Integrante 1/T e dalla Invertibilità (dS=δQ/T)⇔(δQ=TdS) all’INFINITESIMO "δQ", che può diventare un generico Scambio di CALORE Qg=òg(δQ), oppure il DIFFERENZIALE δQ=dQ di determinate PRIMITIVE Termiche (12), ΔQ=∫TdS.

In particolare nelle ISOBARICHE (dp=0) e nelle ISOCORE (dv=0), dove δQ equivale alla ENTALPIA (δQ)p=(dH)p e alla ENERGIA-INTERNA (δQ)v=(dU)v, inoltre nei GENERATORI di VAPORE (dp=0),(dv=0), come le (14),(15).

Infine, l’INTEGRAZIONE (13) in Termini Finiti ∆S=∫(δQ/T) dimostra che l’ENTROPIA dS=δQ/T risulta generalmente INDIPENDENTE dagli SCAMBI TERMICI, Qg=∫g(δQ), ΔQ=∫TdS, e quindi non può rappresentare l’ESPRESSIONE MATEMATICA del SECONDO PRINCIPIO, nemmeno nelle Condizioni di INVERTIBILITA’ (dS=δQ/T)⇔(δQ=TdS), avendo DIMOSTRATO che, a causa della CATENA CINEMATICA, la FORMA del CICLO di CARNOT (Invertibile) viene CONDIZIONATA dal MOTORE TERMICO che lo GESTISCE.

La misteriosa ENTROPIA sperimentale (dS=δQ/T) inizialmente definita da CARNOT-CLAUSIUS l’abbiamo INTEGRATA (link.02) in una FUNZIONE di STATO ΔS=∫δQ/T=f(x,y) che IGNORA gli SCAMBI TERMICI (δQ≠0) e quindi, in linea di principio, con assoluta CERTEZZA risulta INDIPENDENTE dal SECONDO PRINCIPIO della TERMODINAMICA, un ipotetico POSTULATO ancora da DIMOSTRARE.