(06)
Cicli Entalpici MACCHINE TERMICHE A VAPORE, MOTORI E DISTILLATORI

Sintesi del Secondo Brevetto (fig.1,3,5)

INTRODUZIONE

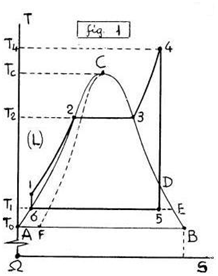
Nel Piano Entropico Ω(T,S) il MISCUGLIO (M) di un LIQUIDO (M’) col suo VAPORE (M”) di TITOLO x=(M”/M) si trova (fig.1) nella ZONA (ACBA), confinante con la ZONA (L) del LIQUIDO situata a sinistra di (AC) e la ZONA (V) del VAPORE Surriscaldato situata a destra di (CB), separate in alto dalla ISOTERMA Inferiore (TC) del GAS (Reale, Ideale) tangente nel PUNTO CRITICO (C) di (ACBA), trascurando il sottostante Miscuglio SOLIDO-VAPORE, poco interessante.

Come ogni FLUIDO anche lo STATO FISICO del Miscuglio dipende (Gibbs) da 2 VARIABILI, come conferma la seguente Equazione Differenziale di CLAPEYRON che lega le tre GRANDEZZE Pressione, Temperatura, Titolo (p,T,x) con EQUAZIONI di STATO del tipo φ(p,T,x)=0, tenuto conto del CALORE di Trasformazione r=r(T,x), del VOLUME SPECIFICO del VAPORE v”=v”(T,x) e del LIQUIDO v’=v’(T,x), anch'esse FUNZIONI di STATO:

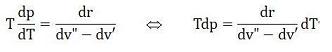
Essa definisce le Trasformazioni IsoTermoBariche (dT=0)⇔(dp=0), dove a ogni Trasformazione ISOTERMICA (dT=0) della Temperatura corrisponde una Trasformazione ISOBARICA (dp=0) della Pressione e viceversa, un vincolo che sussiste senza tener conto delle altre GRANDEZZE Fisiche (Volume,Titolo, Entalpia, Entropia, ecc.), ignorandole come se non esistessero.

In questi casi (dT=0)⇔(dp=0) lo STATO FISICO del Miscuglio (M=M'+M”) assume un particolare Equilibrio Termodinamico chiamato VAPORE SATURO, che nel Piano Entropico Ω(T,S) sussiste lungo qualsiasi linea orizzontale della ZONA (ACBA), dove l’AGGIUNTA o la SOTTRAZIONE di CALORE produce EVAPORAZIONE (dx>0) o CONDENSAZIONE (dx<0) in TUTTA la MASSA del MISCUGLIO creando il ben noto fenomeno fisico chiamato EBOLLIZIONE, con la conseguente variazione del TITOLO (x=M”/M) nell’Intervallo (0≤x≤1).

Peraltro tutte le Trasformazioni φ(p,T,xO)=0 a TITOLO Costante (x0), senza AGGIUNTE o SOTTRAZIONI di Miscuglio, si svolgono necessariamente lungo le CURVE ISOTITOLO (dx=0) di (ACBA), dove ad ogni Incremento ISOTERMICO di PRESSIONE (dT=0),(Δp>0) può aggiungersi il corrispondente Incremento ISOBARICO di TEMPERATURA (dp=0),(ΔT>0) o viceversa, entrambi compresi fra due Isotermo-Isobariche (dT=0)(dp=0)(orizzontali) del VAPORE SATURO.

Questi Incrementi, (dT=0),(Δp>0) o (dp=0),(ΔT>0), avvengono quando la Condensazione (o l’Evaporazione) del Miscuglio si ARRESTA in un PUNTO qualsiasi dell’INTERVALLO (0≤x≤1), sulle orizzontali del VAPORE SATURO, e confermano l’ipotesi che il PRIMO LATO del CICLO RANKINE non appartiene (come si crede) alla ZONA LIQUIDA ma si svolge effettivamente sulla PRIMA ISOTITOLO (x=0) di (ACBA).

Questo accade anche nei PRIMI LATI dei particolari CICLI TERMICI che abbiamo chiamato CICLI ENTALPICI e CICLI ENTROPICI, impropriamente considerati (per similitudine) come VARIANTI del Ciclo RANKINE. Quindi anche in questi due CICLI il Primo Lato non si svolge nella Zona Liquida ma (per quanto precede) su CURVA ISOTITOLO (dx=0) della Zona (ACBA).

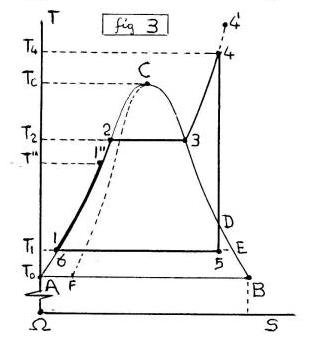
In questa Pagina ci occupiamo dei CICLI ENTALPICI (fig.3,5), MOTORI (fig.3) e DISTILLATORI (fig.5), ottenuti partendo dal CICLO HIRN (fig.3) e dalla relativa Trasformazione Termico-Isobara (ΔT>0),(dp=0),(1,2,3,4,4') estesa fino al VAPORE Surriscaldato, parte del quale (4,4') viene utilizzato per Incrementare l’ENTALPIA (ΔH>0) del LIQUIDO sulla prima Isotitolo (x=0), Riscaldando (dT>0) e Comprimendo (dp>0) secondo la precedente Equazione di CLAPEYRON.

In tal modo si SPOSTANO verso il PUNTO CRITICO (C) le due Isotermo-Bariche (dT=0),(dp=0) orizzontali (2-3),(5-6) del VAPORE SATURO diminuendo l'AREA racchiusa (fig.3,5), cioè LAVORO Utile e RENDIMENTO.

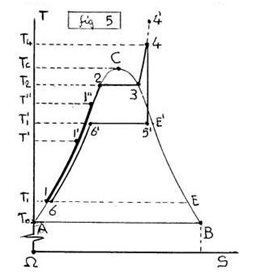
Peraltro, accostando il più possibile al PUNTO CRITICO (C) quelle due IsoTermoBariche (dT=0)(dp=0), si ottengono i CICLI ENTALPICI dei DISTILLATORI (fig.6), dove il CALORE di CONDENSAZIONE può riscaldare in controcorrente il nuovo LIQUIDO che attraversa la IsoTitolo (x=0) del PRIMO LATO.

Inoltre l’equivalente massa di CONDENSATO si RAFFREDDA alla stessa TEMPERATURA del LIQUIDO entrante, pronto per essere UTILIZZATO, a parte quel poco LAVORO disponibile (Area del Ciclo) che può essere dimensionato in modo tale da rendere AUTONOMO l’IMPIANTO, ottenendo infine un DISTILLATO (Acqua Potabile) quasi GRATUITO, tenuto conto del Calore Residuo fornito dall’esterno.

Sostanzialmente l’idea del DISTILLATORE (fig.5) è quella di costruire un piccolo CICLO ENTALPICO in prossimità del PUNTO CRITICO (C), alimentato da nuovo LIQUIDO che entra a BASSA Temperatura e viene RISCALDATO in controcorrente dal CALORE di Condensazione e da VAPORE Surriscaldato lungo la prima Isotitolo (x=0), trasformando il LIQUIDO in DISTILLATO alla Temperatura di Entrata.

Peraltro, escludendo il VAPORE Surriscaldato (4-4’), si può ottenere lo stesso CICLO ENTALPICO in prossimità del PUNTO CRITICO (C) aumentando la PRESSIONE IsoTermica (Δp>0),(dT=0) nel PUNTO INIZIALE (6-1), inoltre la TEMPERATURA IsoBarica (ΔT>0),(dp=0) del PRIMO LATO (1-2), si ARRESTA l’Espansione Isentropica (4-5’),(dS=0) sulla IsoTermoBarica (5’-6’),(dT=0),(dp=0).

In ogni caso lo scopo è quello di creare un CALORE di CONDENSAZIONE (5’-6’),(fig.5) a TEMPERATURA prossima al PUNTO CRITICO, che poi si cercherà di recuperare RISCALDANDO in controcorrente il LIQUIDO ENTRANTE lungo la Isotitolo (x=0) del PRIMO LATO (1-2).

DESCRIZIONE

Nel Campo (ACBA),(fig.1) il MISCUGLIO M=(M'+M'') di TITOLO x=(M''/M), formato da un LIQUIDO (M') col suo VAPORE (M''), diventa VAPORE SATURO durante le Fasi di EBOLLIZIONE, Evaporazione o Condensazione, a causa del CALORE LATENTE definito dalle Trasformazioni IsoTermoBariche (dT=0),(dp=0) nell’Intervallo (0≤x≤1), sulle Orizzontali di (ACBA). In questi CASI (GIBBS) la COPPIA COSTANTE (T,p) rende COSTANTI anche le altre VARIABILI (Entalpia, Entropia, Titolo, ecc.), le quali (Equazione di CLAPEYRON) risultano INDETERMINATE e possono assumere VALORI ARBITRARI nei rispettivi Intervalli di (ACBA).

In effetti soltanto Prima e/o Dopo le EBOLLIZIONI lo STATO FISICO del Miscuglio dipende (GIBBS) da due VARIABILI, mentre la Terna: Pressione-Temperatura-Titolo è legata con EQUAZIONI del Tipo p=f(T,x).
Quindi tutte le TRASFORMAZIONI p=f(T,xO) a TITOLO Costante (dx=0) si svolgono sulle Curve ISOTITOLO (FC),(dx=0) comprese fra le 2 Curve LIMITI (AC),(BC) di (ACBA), tenendo conto che in questi CASI (dx=0) qualsiasi Incremento ISOTERMO di PRESSIONE (dT=0),(Δp>0) richiede un corrispondente Incremento ISOBARO di TEMPERATURA (dp=0),(ΔT>0), o VICEVERSA, fino al ripristino di altre EBOLLIZIONI.

Sono QUESTE le Principali NOVITA’, con prevedibili Conseguenze TERMODINAMICHE.

Sappiamo inoltre (fig.1) che il PRIMO Lato (1-2),(x=0),(dp=0),(ΔT>0), del CICLO RANKINE (1→2→3→4,→5→6=1) non si trova nella Zona Liquida (L) ma sulla Isotitolo (AC),(x=0) di (ACBA) dove il LIQUIDO (M'), a contatto col suo VAPORE (M''), incrementa il Miscuglio (M) nel GENERATORE (G) PRIMA della EBOLLIZIONE.

Lo stesso ACCADE (fig.3,5) ai Primi Lati (1-2),(x=0),(dp=0),(ΔT>0) di Nuovi (inattesi) CICLI TERMICI chiamati CICLI ENTALPICI, MOTORI (1→2→3→4→5→6=1),(fig.3) e DISTILLATORI (1→2→3→4→5'→6'→6=1),(fig.5), a causa della ENTALPIA (H) del LIQUIDO che può essere OTTIMIZZATA sulla Isotitolo (AC),(x=0), ottenendo 2 RECUPERI di CALORE (1-1'),(1-1''),(linee in grassetto) da Alta a Bassa Temperatura (4-4') in (5'-6')→(6'-6), con Crescita del RENDIMENTO del 30-40% nei MOTORI fino al valore UNITARIO nei DISTILLATORI.

In particolare il DISTILLATORE (fig.5,6) può RICICLARE tutto il CALORE di CONDENSAZIONE (1-1′)=(5′-6′), assorbendo da un’UNICA SORGENTE quanto BASTA per ottenere il DISTILLATO (Acqua Potabile) e l’eventuale LAVORO, da GAS (4-5′),(p2→p’) e IDRAULICO (6=1),(p’→p1), dopo la Compressione Iniziale (6=1),(p1→p2). In sostanza si tratta di MODIFICARE la TERMODINAMICA dell’attuale Ciclo RANKINE.

SORGE dunque una VERITA’ sperimentale che metterà in discussione l’ENTROPIA di CLAUSIUS, un insolito DIFFERENZIALE dS=δQ/T che in questi CASI (x=0) lega lo SCAMBIO TERMICO (δQ) alla ENTALPIA (δQ)p=(dH)p del LIQUIDO, facendo crescere il RENDIMENTO.

Si INTUISCE dunque che NON SEMPRE (o forse MAI) l’ENTROPIA dS=δQ/T può rappresentare l’UNICA ESPRESSIONE MATEMATICA del SECONDO PRINCIPIO della TERMODINAMICA.

(6→1→2→3→4→5→6)⇒(6→2→3→4→5→6)⇒(1→2→3→4→5'→6'→1)