(08)
CRITERI DI OTTIMAZIONE DEL RENDIMENTO
DI UN MOTORE PRIMO TERMICO
Sintesi del Quarto Brevetto (fig.6)
INTRODUZIONE
Il CALORE è classificato ENERGIA di SECONDA SPECIE perché può compiere LAVORO CICLICO (ripetibile periodicamente) soltanto tramite MOTORI TERMICI, costituiti essenzialmente da una CAMERA di Combustione dove si svolgono i Cicli PRIMARI nel Piano Entropico Ω(T,S) e da un ALBERO MOTORE dove si realizzano i corrispondenti Cicli INDOTTI nel Piano Meccanico O(F,s), trasformando CALORE in ENERGIA di PRIMA SPECIE.
Essi sono collegati da una Trasmissione Meccanica chiamata CATENA CINEMATICA, formata da pochi elementi statici (Condotti, Valvole, ecc.) nelle TURBINE e dal Meccanismo BIELLA MANOVELLA nei MOTORI Alternativi.
In tutti questi casi la CATENA CINEMATICA modifica notevolmente la TERMODINAMICA e i RENDIMENTI dei CICLI TERMICI anche e non solo a causa degli ATTRITI, specialmente nei MOTORI ALTERNATIVI, dove si verifica diminuzione del RENDIMENTO rispetto alle TURBINE a GAS di uguale POTENZA, come cercheremo di dimostrare.
Nel seguito ci occupiamo delle CATENE CINEMATICHE dei MOTORI TERMICI, specialmente ALTERNATIVI, cioè dei MECCANISMI (pistoni, leve, cinghie, ruotismi, ecc.) che collegano la CAMERA di Combustione all’ALBERO, impiegati allo scopo di trasformare la PRESSIONE del GAS in FORZA MOTRICE, dimostrando contro ogni previsione che quei COLLEGAMENTI condizionano la TERMODINAMICA e il RENDIMENTO dei MOTORI.
In effetti le CATENE CINEMATICHE modificano il RENDIMENTO dei MOTORI TERMICI, specie Alternativi, lasciando INVARIATO quello dei MOTORI Meccanici, UNITARIO in assenza di ATTRITI.
In particolare MODIFICANDO opportunamente il Meccanismo BIELLA MANOVELLA si può migliorare il RENDIMENTO dei MOTORI Alternativi fino a SUPERARE quello TEORICO calcolato nella Camera di Combustione.
Questi RISULTATI (inattesi quanto imprevedibili) mettono in discussione alcuni importanti TEOREMI di FISICA SPERIMENTALE, in particolare la VALIDITA' del Postulato di CARNOT-CLAUSIUS (Secondo Principio della Termodinamica) e il suo legame con la FUNZIONE di STATO chiamata ENTROPIA, tenendo conto che anche il RENDIMENTO del CICLO di CARNOT invertibile viene condizionato da una CATENA CINEMATICA. Si tratta dei principali argomenti di una TESI di LAUREA avente per TITOLO: "CRITERI DI OTTIMAIONE DEL RENDIMENTO DI UN MOTORE PRIMO TERMICO", che poi (in appendice) sconfinava in una LEGGE ASSOLUTA applicabile per via sperimentale, assieme alle modifiche di altri TEOREMI ritenuti intoccabili, in particolare il CONCETTO di INTEGRALE INDEFINITO (o PRIMITIVA) di una FUNZIONE CONTINUA.
DESCRIZIONE
All’inizio si trattava di CAPIRE perché i MOTORI Termici Alternativi non sono più ECONOMICI delle TURBINE a GAS di uguale POTENZA pur essendo più alti i RENDIMENTI dei Cicli IDEALI mentre gli ATTRITI sono quasi IDENTICI.
La DISCORDANZA dipende dalla DIVERSITA’ delle due MACCHINE, cioè dalla CATENA CINEMATICA che collega la CAMERA di Combustione all’ALBERO, quasi INESISTENTE nelle TURBINE mentre nei MOTORI ALTERNATIVI è formata dal MECCANISMO BIELLA MANOVELLA, dove le FORZE Termiche diventano MASSIME nei PUNTI MORTI quando la loro UTILITA’ è NULLA.
In effetti nelle MODALITA’ di REGIME (dopo la messa in MOTO) ogni MOTORE a COMBUSTIONE INTERNA funziona da SOLO, in MODO AUTONOMO, INDIPENDENTE, a SCATOLA CHIUSA, quindi AUTOGESTISCE in TEMPI REALI (Istante per Istante) il BILANCIO ENERETICO di CALORE δQ e LAVORO δL con l’ESTERNO.
Essa definisce le Trasformazioni ISOTERMO-ISOBARICHE (dT=0)⇔(dp=0), dove a ogni Trasformazione ISOTERMICA (dT=0) della Temperatura corrisponde una Trasformazione ISOBARICHA (dp=0) della Pressione e viceversa, un vincolo che sussiste per qualsiasi valore delle altre GRANDEZZE (Volume,Titolo, Entalpia, Entropia, ecc.), che possono ignorarsi.
Si INTUISCE che il RENDIMENTO può essere OTTIMIZZATO MODIFICANDO opportunamente il MECCANISMO.
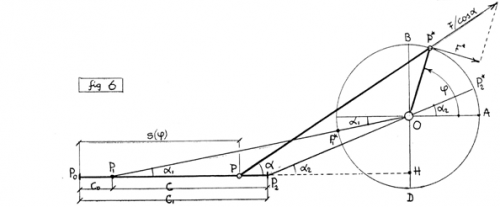
Nei MOTORI ALTERNATIVI (a Scoppio, Diesel) questo si ottiene TRASLANDO l’ALBERO ad una determinata DISTANZA h=(OH)<(OD) dall’ASSE (PH) del CILINDRO, affinché (durante il MOTO) risulti MASSIMA la FASE di ESPANSIONE ANGOLARE nel VERSO positivo di ROTAZIONE (AOP*):
(π+α1)≤φ≤(2π+α2)
Il PROBLEMA è soltanto QUANTITATIVO, quindi per RISOLVERLO occorreva SEPARARE le GRANDEZZE TERMICHE prodotte nel CILINDRO da quelle MECCANICHE che il MECCANISMO tramette all'ALBERO, già risolte nei POTENZIALI TERMODINAMICI (Energia-Interna, Entalpia, ecc.), intuendo che (malgrado l'apparenza del SIMBOLISMO) l’ENTROPIA dS=δQ/T e lo SCAMBIO TERMICO δQ sono due INFINITESIMI INDIPENDENTI.
Peraltro l'ENTROPIA dS=δQ/T è certamente un DIFFERENZIALE ESATTO. Infatti lo abbiamo INTEGRATO in Termini Finiti con EQUAZIONI di STATO del Tipo ΔS=f(F,s)=g(p,V) nei Piani Meccanici O(F,s),O(p,V), dove le IsoEntropiche (dS=0) formano un insieme di Curve INTEGRALI f(F,s)=g(p,V)=Cost non ADIABATICHE (δQ≠0).
Tuttavia, in certe TRASFORMAZIONI (dS=δQ/T)⇔(δQ=TdS) anche lo SCAMBIO TERMICO (δQ) diventa un DIFFERENZIALE δQ=dQ=TdS, in particolare nelle ISOCORE (dV=0) e/o nelle ISOBARE (dp=0), dove (δQ) equivale alla ENERGIA INTERNA (δQ=kdU)V e/o alla ENTALPIA (δQ=dH)p, inoltre nei Generatori di VAPORE (dV=0),(dp=0), con prevedibili conseguenze FISICO-MATEMATICHE, specialmente TERMODINAMICHE.
Con queste PREMESSE siamo giunti alla OTTIMAZIONE dei MOTORI TERMICI ALTERNATIVI, dove i RENDIMENTI possono CRESCERE del 20-30%, a volte superando quelli dei CICLI-IDEALI svolti nei rispettivi CILINDRI.
Anche la MACCHINA PERFETTA di CARNOT (priva di Attriti) è dotata di MECCANISMI, le cui MODIFICHE possono cambiare il RENDIMENTO. Quindi il Ciclo di CARNOT dipende dalla MACCHINA TERMICA che lo GESTISCE.
Insomma l’ENTROPIA di CLAUSIUS dS=δQ/T non può rappresentare l’UNICA Espressione Matematica SECONDO PRINCIPIO DELLA TERMODINAMICA, nemmeno nelle suddette Condizioni di INVERTIBILITA’ (dS=δQ/T)⇔(δQ=TdS) dei due INFINITESIMI (dS,δQ), quando anche lo SCAMBIO TERMICO (δQ) diventa un DIFFERENZIALE dQ=δQ=TdS.