(10)
MACCHINE TERMICHE A VAPORE Cicli Entalpici, Motori e Distillatori

Versione integrale del secondo Brevetto, Attestato (link.18)

Cicli ENTALPICI ⇔ (1→2→3→5→6) ⇔ (1→2→3→4→5'→6'→6)

INTRODUZIONE

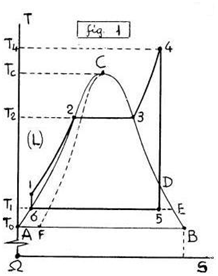
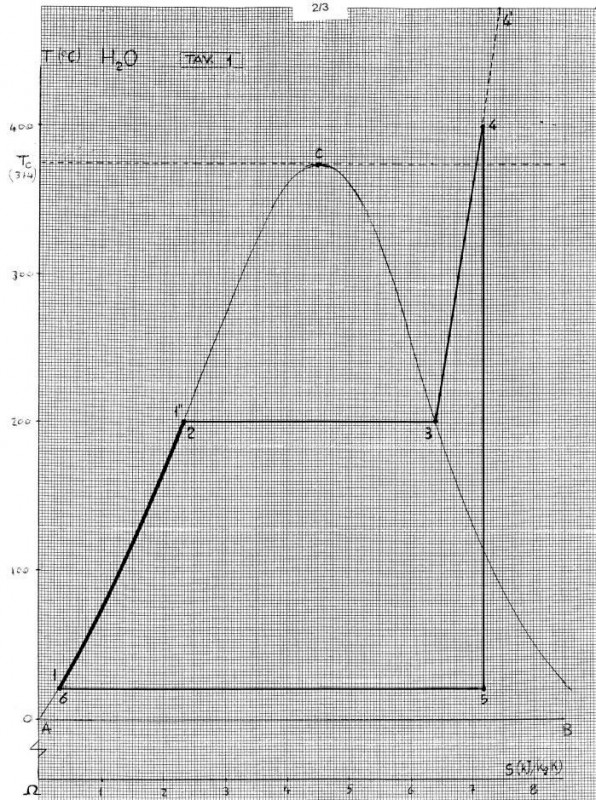
Nel Piano Entropico Ω(T,S) il MISCUGLIO (M) di un LIQUIDO (M’) col suo VAPORE (M”) di TITOLO x=(M”/M) si trova (fig.1) nella ZONA (ACBA), confinante con la ZONA (L) del LIQUIDO situata a sinistra di (AC) e la ZONA (V) del VAPORE Surriscaldato situata a destra di (CB), separate in alto dalla ISOTERMA Inferiore (TC) del GAS tangente nel PUNTO CRITICO (C) di (ACBA), trascurando il sottostante Miscuglio SOLIDO-VAPORE.

Come ogni FLUIDO anche lo STATO FISICO del Miscuglio dipende (Gibbs) da 2 VARIABILI, come conferma la seguente Equazione Differenziale di CLAPEYRON che lega le tre GRANDEZZE Pressione, Temperatura, Titolo (p,T,x) con EQUAZIONI di STATO del tipo φ(p,T,x)=0, tenuto conto del CALORE di Trasformazione r=r(T,x), del VOLUME SPECIFICO del VAPORE v”=v”(T,x) e del LIQUIDO v’=v’(T,x), anch'esse FUNZIONI di STATO:

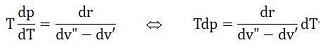
φ(p,T,x)=0

Essa definisce le Trasformazioni IsoTermoBariche (dT=0)⇔(dp=0), dove a ogni Trasformazione ISOTERMICA (dT=0) corrisponde una Trasformazione ISOBARICA (dp=0) e viceversa, un vincolo Termodinamico che sussiste per qualsiasi valore delle altre GRANDEZZE Fisiche (Volume,Titolo, Entalpia, Entropia, ecc.) che vengono ignorate, come se non esistessero.

In questi casi (dT=0)⇔(dp=0) lo STATO FISICO del Miscuglio (M=M'+M”) assume un particolare Equilibrio Termodinamico chiamato VAPORE SATURO, che nel Piano Entropico Ω(T,S) sussiste lungo qualsiasi linea orizzontale della ZONA (ACBA), dove l’AGGIUNTA o la SOTTRAZIONE di CALORE produce EVAPORAZIONE (dx>0) o CONDENSAZIONE (dx<0) in TUTTA la MASSA del MISCUGLIO creando il ben noto fenomeno fisico chiamato EBOLLIZIONE, con la conseguente variazione del TITOLO (x=M”/M) nell’Intervallo (0≤x≤1).

Peraltro tutte le Trasformazioni φ(p,T,xO)=0 a TITOLO Costante (x0), senza AGGIUNTE o SOTTRAZIONI di Miscuglio, si svolgono necessariamente lungo le CURVE ISOTITOLO (dx=0) di (ACBA), dove ad ogni Incremento ISOTERMICO di PRESSIONE (dT=0),(Δp>0) può aggiungersi il corrispondente Incremento ISOBARICO di TEMPERATURA (dp=0),(ΔT>0) o viceversa, entrambi compresi fra due Isotermo-Isobariche (dT=0)(dp=0)(orizzontali) del VAPORE SATURO.

Questi Incrementi, (dT=0),(Δp>0) o (dp=0),(ΔT>0), avvengono quando la CONDENSAZIONE (o l’Evaporazione) del MISCUGLIO si ARRESTA in un PUNTO qualsiasi dell’INTERVALLO (0≤x≤1), sulle orizzontali del VAPORE SATURO, e confermano l’ipotesi che il PRIMO LATO del Ciclo RANKINE non si trova nella Zona LIQUIDA ma sulla Prima IsoTitolo (x=0) di (ACBA).

Questo accade anche nei PRIMI LATI di particolari CICLI TERMICI che abbiamo chiamato CICLI ENTALPICI e CICLI ENTROPICI, che sono VARIANTI del Ciclo RANKINE. Anche in questi due Cicli il PRIMO LATO non si trova nella Zona Liquida ma sulla prima Curva IsoTitolo (dx=0) di (ACBA).

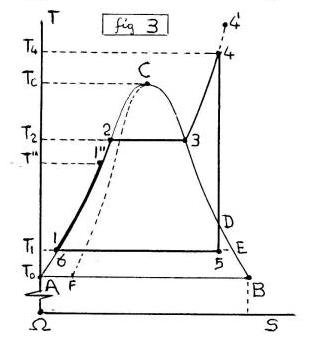
In questa Pagina ci occupiamo dei CICLI ENTALPICI (fig.3,5), MOTORI (fig.3) e DISTILLATORI (fig.5), partendo dal CICLO HIRN (fig.3) e dalla Trasformazione Termo-Isobara (ΔT>0),(dp=0),(1,2,3,4,4') estesa al VAPORE Surriscaldato, parte del quale (4-4') Incrementa l’ENTALPIA (ΔH>0) del LIQUIDO sulla Pma Isotitolo (x=0), Riscaldando (ΔT>0) e Comprimendo (Δp>0) secondo l’Equazione di CLAPEYRON φ(p,T,xO)=0.

In tal modo si SPOSTANO in ALTO le due IsoTermoBariche (dT=0),(dp=0),(2-3),(5-6) del VAPORE SATURO avvicinandosi al PUNTO CRITICO (C), quindi diminuisce l'AREA Racchiusa, il LAVORO Utile e il RENDIMENTO dei Cicli ENTALPICI (fig.3,5).

Accostando al PUNTO CRITICO (C) le due Isotermo-Bariche (dT=0)(dp=0), si ottengono i CICLI ENTALPICI dei DISTILLATORI (fig.6), dove il CALORE di Condensazione RISCALDA in Controcorrente il nuovo LIQUIDO sulla Isotitolo (x=0) del PRIMO lato.

Quindi l’equivalente CONDENSATO si raffredda alla stessa TEMPERATURA del LIQUIDO entrante, pronto per essere utilizzato, a parte quel poco LAVORO disponibile (Area del Ciclo) che può essere DIMENSIONATO in modo da rendere AUTONOMO l’IMPIANTO, ottenendo infine un DISTILLATO (Acqua Potabile) quasi GRATUITO, tenuto conto del CALORE fornito dall’ESTERNO.

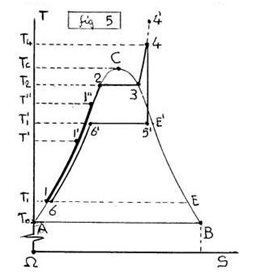
L’idea del DISTILLATORE (fig.5) è stata quella di COSTRUIRE un piccolo CICLO ENTALPICO in prossimità del PUNTO CRITICO (C), con nuovo LIQUIDO che entra a BASSA Temperatura e RISCALDATO in controcorrente dal CALORE di Condensazione e da VAPORE SURRISCALDATO sulla ISOTITOLO (x=0) del PRIMO Lato, dove il LIQUIDO si TRASFORMA in DISTILLATO alla stesa TEMPERATURA di ENTRATA.

Peraltro, escludendo il VAPORE Surriscaldato (4-4’), si può ottenere un CICLO ENTALPICO in prossimità del PUNTO CRITICO aumentando la PRESSIONE ISOTERMICA (Δp>0),(dT=0) nel PUNTO INIZIALE (6-1) e poi la TEMPERATURA ISOBARICA (ΔT>0),(dp=0) del PRIMO LATO (1-2), infine si ARRESTA l’ESPANSIONE ISENTROPICA (4-5’),(dS=0) sulla nuova ISOTERMO-BARICA (5’-6’),(dT=0),(dp=0).

Comunque lo scopo è quello di ottenere un CALORE di Condensazione (5’-6’),(fig.5) a TEMPERATURA prossima al PUNTO CRITICO, che si cercherà di utilizzare RISCALDANDO in controcorrente il LIQUIDO entrante lungo la ISOTITOLO (x=0) del PRIMO Lato (1-2).

RIASSUNTO (fig.1,3,5)

Nel Campo (ACBA),(fig.1) il MISCUGLIO M=(M'+M'') di TITOLO x=M''/M, formato da un LIQUIDO M' col suo VAPORE M'', diventa VAPORE SATURO durante le FASI di EBOLLIZIONE, a causa del CALORE LATENTE creato dalle IsoTermoBariche (dT=0),(dp=0) nei Sottoinsiemi dell’Intervallo (0≤x≤1), sulle orizzontali di (ACBA).

Con queste IPOTESI lo STATO FISICO del MISCUGLIO dipende (Gibbs) da due VARIABILI, quindi la TERNA (Pressione-Temperatura-Titolo) è legata (CLAPEYRON) con EQUAZIONI del tipo p=f(T,x). In particolare tutte le

TRASFORMAZIONI p=f(T,x0) a TITOLO Costante (dx=0) si svolgono sulle ISOTITOLO (FC),(dx=0) comprese fra le due CURVE LIMITI (AC),(BC) di (ACBA), tenendo conto che in questi casi (dx=0) ogni Incremento IsoTermico di PRESSIONE (dT=0),(Δp≠0) richiede un Incremento ISOBARICO di TEMPERATURA (dp=0)(ΔT≠0) e viceversa, fino al ripristino di altre EBOLLIZIONI, sulle orizzontali di (ACBA).

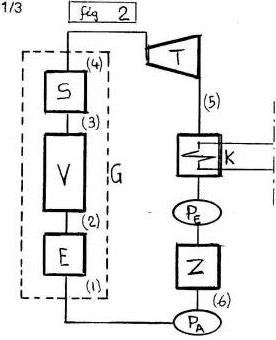
Fra l’ALTRO, il PRIMO Lato (1-2),(dp=0) del CICLO RANKINE-HIRN (fig.1,2) appartiene alla PRIMA Isotitolo (AC),(x=0) di (ACBA), come pure i PRIMI Lati (1-2),(dp=0) dei nuovi CICLI TERMICI (fig.3,5), che abbiamo chiamato Cicli ENTALPICI: MOTORI (1→2→3→4→5→6=1) e DISTILLATORI (1→2→3→4→5→5'→6'→6=1), (fig.5).

Peraltro l'ENTALPIA (H) del LIQUIDO può essere OTTIMIZZATA spostandola sulla prima ISOTITOLO (AC),(x=0) di (ACBA) aggiungendo anche (fig.5) due RECUPERI di CALORE (1-1'),(1-1''),(in grassetto), con la conseguente CRESCITA del RENDIMENTO dal 30-40% nei MOTORI fino al valore UNITARIO nei DISTILLATORI. Soprattutto (fig.5,6) il DISTILLATORE può RICICLARE tutto il CALORE di CONDENSAZIONE (1-1')=(5'-6'), assorbendo da un’UNICA SORGENTE TERMICA quanto BASTA per ottenere il DISTILLATO (Acqua Potabile) e l’eventuale LAVORO, da GAS (4-5'),(p2→p') e IDRAULICO (6-1),(p'→p1), che rende l'IMPIANTO AUTONOMO da altre FONTI di CALORE. Si tratta di MODIFICARE opportunamente la TERMODINAMICA del CICLO RANKINE-HIR.

DESCRIZIONE

Nel Campo (ACBA),(fig.1) il MISCUGLIO M=(M'+M'') di TITOLO x=M''/M, formato da un LIQUIDO M' col suo VAPORE M'', diventa VAPORE durante le Fasi di EBOLLIZIONE, a causa del CALORE LATENTE creato nelle IsoTermoBariche (dT=0),(dp=0) nell’Intervallo (0≤x≤1) di (ACBA), dove (Gibbs) la Coppia Costante (T,p) rende COSTANTI le altre VARIABILI (Entalpia, Entropia, Titolo, ecc.), che restano (Clapeyron) ARBITRARIE.

In effetti soltanto PRIMA e/o DOPO le EBOLLIZIONI lo STATO FISICO del MISCUGLIO dipende (GIBBS) da due VARIABILI, quindi la TERNA (Pressione, Temperatura, Titolo) è LEGATA con EQUAZIONI del tipo p=f(T,x).

Peraltro tutte le TRASFORMAZIONI p=f(T,x0) a TITOLO Costante (dx=0) si svolgono sulle IsoTitolo (FC),(dx=0) comprese fra le due CURVE Limiti (AC),(BC) di (ACBA) fino al ripristino delle EBOLLIZIONI. In questi casi (dx=0) ogni Incremento IsoTermico di PRESSIONE (dT=0),(Δp>0) richiede un Incremento IsoBaro di TEMPERATURA (dp=0),(ΔT>0), essendo p=f(T,x0),(dx=0), ∀(FC)∈(ACBA). Queste NOVITA’ consentono notevoli conseguenze.

Fra l’Altro il Primo LATO (1-2),(dp=0),(x=0) del CICLO HIRN (1→2→3→4→5→6=1),(fig.1) non si trova (come si crede) nella Zona LIQUIDA (L) ma sulla Prima ISOTITOLO (AC),(x=0) di (ACBA) dove il LIQUIDO (M'), sempre a contatto col suo VAPORE (M''), incrementa il MISCUGLIO (M) nel GENERATORE (G) PRIMA della EBOLLIZIONE.

E’ quanto ACCADE anche ai PRIMI LATI (1-2),(dp=0),(x=0) di (inattesi) nuovi CICLI TERMICI (fig.3,5), chiamati CICLI ENTALPICI, MOTORI (1→2→3→4→5→6=1),(fig.3) e DISTILLATORI (1→2→3→4→5→5'→6'→6=1)(fig.5), a causa della ENTALPIA (H) del LIQUIDO che può essere OTTIMIZZATA spostandola sulla Prima ISOTITOLO (AC),(x=0) di (ACBA), ottenendo 2 RECUPERI di CALORE (1-1'),(1-1''),(linee in grassetto) con la conseguente CRESCITA del RENDIMENTO dal 30-40% nei MOTORI fino a diventare UNITARIO nei DISTILLATORI.

In particolare (fig.5,6) il DISTILLATORE può RICICLARE il CALORE di Condensazione (1-1′)=(5′-6′) assorbendo da un’UNICA SORGENTE quanto BASTA per ottenere il DISTILLATO (Acqua Potabile) e l’eventuale LAVORO da GAS (4-5′),(p₂→p‘) e IDRAULICO (6=1),(p’→p₁) che rende l’IMPIANTO autonomo da altre FONTI di CALORE.

Si tratta di MODIFICARE opportunamente la TERMODINAMICA del Ciclo RANKINE. Infatti per TRACCIARLI (Tab.A),(Tav.1,2),(fig.1,3,5) ci siamo valsi delle 5 VARIABILI (p,v,T,H,S) legate dal POTENZIALE ENTALPICO dH=δQ+vdp, che definiscono le Trasformazioni ISOBARE dp=0, ADIABATICHE δQ=0, infine il BILANCIO TERMICO (Q1),(Q2) e il RENDIMENTO (η) dell’IMPIANTO, in funzione delle 3 Grandezze ENTALPICHE (H1,H4,H5):

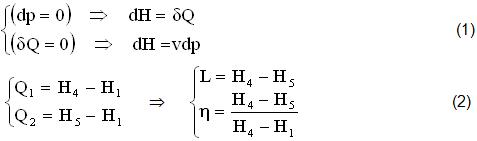
Ma il LAVORO L=(H₄-H₅) non dipende dalla ENTALPIA (H₁), che può variare (H*≠H₁) sulla Curva Limite ξ‘=(AC),(x=0) del LIQUIDO (M’) con i seguenti valori del RENDIMENTO (η*≠ η):

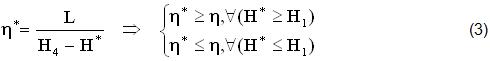
Questo significa (fig.3,5) che l’ENTALPIA (H₁) del LIQUIDO può OTTIMIZZARSI (H*) sulla CURVA Limite (AC),(x=0), ottenendo (linee in grassetto) due RECUPERI di Calore Q*=(H*-H₁)=(1-1”)+(1-1′)>0, quello SENSIBILE Q”=(1-1”)>0 sottratto al VAPORE (4-4′) e quello LATENTE di Condensazione Q’=(1-1′)≥0, entrambi RICICLATI nell’Economizzatore (E), facendo assumere al BILANCIO (2),(3) dei precedenti CICLI (fig.3,5) la seguente FORMA, sapendo che in questi casi (Rivalutazione Termica) c.MΔT kcal possono RICICLARE M kg di H₂O da ZERO a T°C, oppure 2M kg a T/2 °C, in generale n.M kg da ZERO a T/n °C (con n≥1):

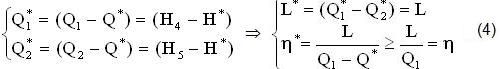
Nascono così (fig.3,5) i suddetti Cicli ENTALPICI, anch’ESSI (come RANKINE) fondati sulle 2 ISOTERMOBARICHE estreme (5-6),(2-3)-(5′-6′),(2-3) del VAPORE SATURO, situate alla massima distanza (5-6)↔(2-3),(fig.3,4) nei MOTORI, oppure (fig.5,6) ravvicinate quasi a coincidere (5′-6′)→(2-3) nei DISTILLATORI, dove il LAVORO (4-5′),(Area-Racchiusa) può diminuire (L→0) quanto BASTA affinché l’IMPIANTO diventi AUTONOMO, con l’eventuale aggiunta di unaTURBINA IDRAULICA (T₀),(p’→p₁).

Descriviamo brevemente i due CICLI ENTALPICI più interessanti (fig.3,5), evidenziando le Trasformazioni ISOTITOLO ISOBARE dei PRIMI Lati (1-2)(x=0),(dp=0)∈(ξ‘=AC),(x=0) inoltre i Recuperi di CALORE Q*=(Q’+Q”)∈(ξ‘) del BILANCIO TERMICO (4), che lasciano invariato il LAVORO (L*= L) ma fanno crescere il RENDIMENTO (η*> η) ∀(Q*>0) nei MOTORI, fino al Valore UNITARIO (η*=1),∀(Q*≥Q₂) nei DISTILLATORI.

A) MOTORE ENTALPICO

(1→2→3→4→5→6≈1), (Tav.1), (fig.3,4).

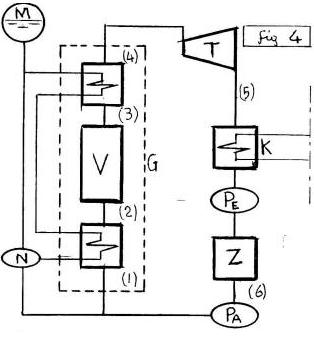
La POMPA (P_A) comprime il LIQUIDO (M’),(Δp>0),(dT=0) nel PUNTO Iniziale (6≈1),(p₁→p₂),(T₁),(x=0), si RISCALDA (in E) sulla ISOTITOLO-ISOBARA (1-2),(p=p₂),(T₁→T₂)∈(ξ‘=AC),(x=0), utilizzando anche il CALORE (1-1”)=(4-4′) sottratto al VAPORE (3-4’), poi EVAPORA sulla IsoTermoBarica (2-3),(p₂),(T₂),(x→1), SURRISCALDA (3-4),(p₂),(T₂→T₄),(x=1), si ESPANDE nella TURBINA (4-5),(p₂→p₁),(T_4→T₁),(x→x₅), infine CONDENSA (in K) lungo la IsoTermoBarica (5-6),(p₁),(T₁),(x→0). Nel Bilancio (4) quel Recupero Q*=(Q”) fa crescere del 30-40% il RENDIMENTO del LAVORO (4-5),(Area Racchiusa).

B) DISTILLATORE ENTALPICO

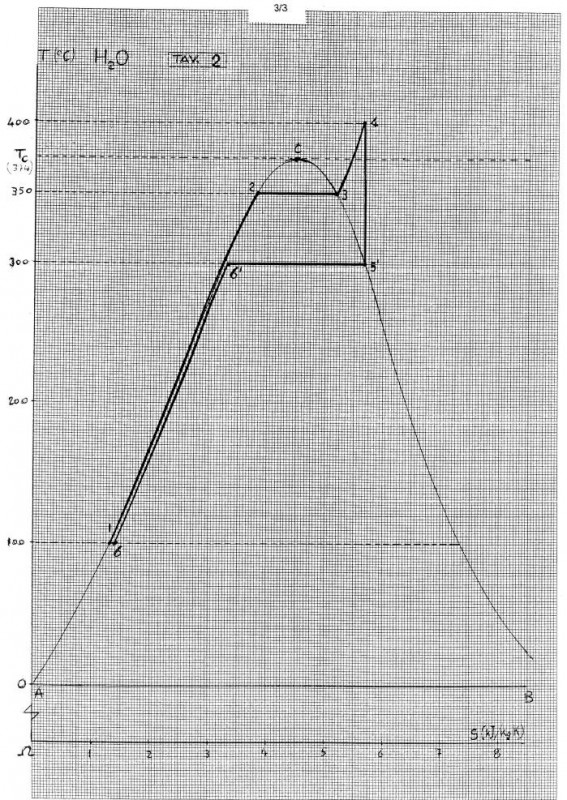
(1→2→3→4→5'→6'→6≈1), (Tav.2), (fig.5,6).

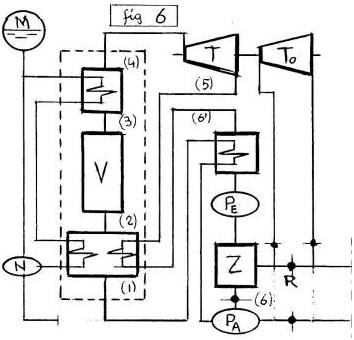
Il LIQUIDO (M’),(p₁)(T₁),(x=0), viene COMPRESSO nel PUNTO Iniziale (6≈1),(p₁→p₂),(T₁), si RISCALDA sulla Isotitolo-Isobarica (1-2),(p₂),(T₁→T₂),(x=0)∈(ξ‘=AC), utilizzando anche il Calore Q”=(1-1”)=(4-4′) sottratto al Vapore (3-4’), quindi Evapora (2-3),(p₂),(T₂),(x→1), Surriscalda (3-4),(p₂),(T₂→T₄),(x=1), poi ESPANDE in TURBINA (4-5′),(p₂→p’),(T₄→T’), infine prosegue la Condensazione IsoTermoBarica (5′-6′),(p’),(T’),(x→0), con l’eventuale impiego del CONDENSATORE (K), cedendo il RECUPERO Q’=(1-1′)≤(5′-6′) al LIQUIDO (M’),(x=0) sulla Isotitolo-Isobarica (x=0),(dp=0),(dT>0),(1-2)∈(AC).

Peraltro il RENDIMENTO UNITARIO (η*=1) si ottiene OTTIMIZZANDO le posizioni delle due IsoTermoBariche (5'-6'),(2-3) rispetto al PUNTO CRITICO, mentre il LAVORO L=(4-5'),(Area Racchiusa) DIMINUISCE (L→0) quanto basta (L>0) affinché il DISTILLATORE diventi AUTONOMO, separando il POTABILE (Z) dal Liquido INQUINATO (PA).

Lo stesso RENDIMENTO UNITARIO (η*=1) si ottiene più facilmente (fig.5,6) a bassa PRESSIONE (p₁< p'< p₂), uguagliando le Aree Sottostanti (Q*= Q₂) alle curve di CONDENSAZIONE (5′-6′) e di RAFFREDDAMENTO (6′-6).

C) DISTILLATORE ENTALPICO SEMPLICE (fig.5,6).

Si tratta del CASO LIMITE (p’→p₂),(L→0), dove conviene sostituire la TURBINA (T) con un RIDUTTORE (R), mentre il RENDIMENTO UNITARIO si ottiene più facilmente RICICLANDO tutto il CALORE di Condensazione (1-1′)=(5′-6′) con l’impiego di entrambi i RECUPERI (Q”+Q’) e di una TURBINA IDRAULICA (T₀),(p’→p₁) che collega il POZZO (Z) al LIQUIDO USCENTE. In sintesi, nei PRIMI Lati (x=0),(p₂),(T₁→T₂),(1-2)∈(AC) dei CICLI ENTALPICI (fig.3,5), l’ ENTALPIA (H) del LIQUIDO può migliorare il BILANCIO TERMICO (4) con uno o entrambi i RECUPERI Q*=(Q”+Q’) RICICLATI nell’ ECONOMIZZATORE (E), facendo crescere il RENDIMENTO (η<1) fino al valore UNITARIO (η*=1).

In particolare il DISTILLATORE può RICICLARE tutto il CALORE di CONDENSAZIONE Q'=(1-1')=(5'-6') con RENDIMENTO UNITARIO, assorbendo da un’UNICA SORGENTE soltanto il CALORE MANCANTE, cioè quanto BASTA per produrre il DISTILLATO (Acqua Potabile) e l’eventuale LAVORO necessario al suo funzionamento.

Per questi MOTIVI previsti in precedenza SORGE dunque una VERITA’ SPERIMENTALE che mette in DISCUSSIONE l’ ENTROPIA di CLAUSIUS dS=δQ/T, un isolito DIFFERENZIALE (dS) indipendente dal generico Scambio di Calore δQ, che diventa un DIFFERENZIALE δQ=dQ=TdS soltanto in particolari TRASFORMAZIONI e quindi non può rappresentare l’ESPRESIONE MATEMATICA del SECONDO PRINCIPIO della TERMODINAMICA.

A questo punto, Certi dell’AFFIDABILITA’ di quanto precede, la RICERCA può dirsi CONCLUSA. Per il RESTO conviene approfondire in altra SEDE lo STUDIO, le possibili APPLICAZIONI e la Scelta dei più opportuni FLUIDI TERMODINAMICI.

Tuttavia (anche se non necessario) faremo alcuni ESEMPI orientativi dei preceden CICLI ENTALPICI A),B),C) relativi all’ACQUA (H₂O), con i BILANCI TERMICI (2),(4), utilizzando la seguente Tabella A e le EQUAZIONI Comparative (5) che legano il TITOLO (x), l’ENTROPIA (S_X) e l’ENTALPIA (H_X) del MISCUGLIO (M), a parte l’ipotetica PORTATA m=10(kg/s)=0,1(kg/Ciclo), RIPARTITA ad esempio in 100(Cicli/s), che determina la POTENZA media N=mL(kW) e la GRANDEZZA dell’IMPIANTO.

T (⁰C)	p (K_p/cm²)	H¹ (kJ/kg)	Hⁿ (kJ/kg)	Hⁿ-H¹ (kJ/kg)	S¹ (kJ/kgK)	Sⁿ (kJ/kgK)
374,15	225,6	2100	2100	0	4,430	4,430
350 (400)	168,6	1671	2564 (2930)	893	3,779	5,212 (5,777)
300 (400)	87,6	1345	2749 (3117)	1404	3,255	5,705 (6,293)
250 (400)	40,6	1086	2801 (3210)	1715	2,793	6,072 (6,770)
200 (400)	16,0	852	2793 (3256)	1941	2,331	6,432 (7,243)
150	4,85	632	2746	2114	1,842	6,838
100	1,033	419	2676	2257	1,307	7,355
50	0,126	209	2592	2383	0,704	8,075
30	0,043	126	2556	2430	0,437	8,452
20	0,024	84	2537	2453	0,296	8,666

PROCEDIMENTO

Nel Piano-Entropico Ω(T,S) abbiamo tracciato (Tab.A),(Tav.1,2) i CICLI-ENTALPICI dell’ACQUA (H₂O) assegnando le due Isotermobariche del VAPORE-SATURO, (5-6),(p₁),(T₁) e (2-3),(p₂),(T₂), inoltre (fuori Tabella) il Surriscaldato T₄(⁰C), H₄(kJ/kg), la Isentropica S₄=S₅(kJ/kgK), le ENTALPIE del Liquido (H’,H”). Quindi, con le (5) calcoliamo le Coordinate di fine Espansione (x₅),(H₅), i RECUPERI di Calore Q*=(Q’,Q”), infine i corrispondenti BILANCI-TERMICI HIRN (2) ed ENTALPICO (4), aventi lo stesso Lavoro (L*=L=H₄-H₅) ma differenti RENDIMENTI (h*>h).

1) CICLO RANCHINE NORMALE

(1→2→3→4→5→6»1) (Tab.A, Tav.1, fig.1,2).

Sulla Isotermobarica inferiore (1-E) si assegnano: T₁=20(⁰C), p₁=0,024(at), H₁=84, H_E=2537, S₁=0,296, S_E=8,666; poi sulla Isotermobarica superiore (2-3): T₂=200(⁰C), p₂=16(at), inoltre (fuori Tabella) T₄=400(⁰C), H₄=3256, S₄=S₅=7,243; poi la Portata m=10(kg/s), infine (5) calcoliamo (x₅),(H₅) e il Bilancio (2) del CICLO-HIRN:

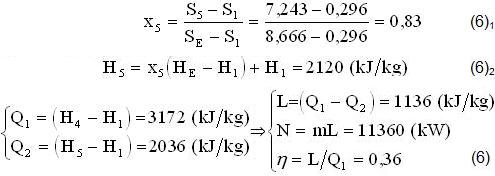
1-A) CICLO ENTALPICO MOTORE

(1→1''→2→3→4→5,6»1) (Tab.A, Tav.1, fig.3,4).

Il più conveniente CICLO-ENTALPICO-MOTORE si ottiene applicando al precedente CICLO-HIRN il massimo RECUPERO di Calore Q”=(1-1”)=(H”-H₁)=(852-84)=768, RICICLATO dalla Zona-Alta (S) alla Zona-Bassa (E) del Generatore (G), con un Rendimento (η*=0,47) che risulta maggiore del 30% rispetto a quello (η=0,36):

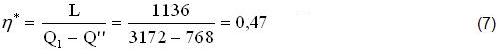
Ulteriore crescita del Rendimento (η*), fino al 30-40%, si ottiene se quei corrispondenti “CICLI-TERMICI” (HIRN e ENTALPICO) occupano Zone più grandi nel Campo (ACBA) del Miscuglio (M).

2) RANKINE SPOSTATO IN ALTO

(1'→2→3→4→5'→6'»1'), (Tab.A, Tav.2, fig.5,6).

Nella Isotermobarica inferiore (6′-E’) si assegnano: T₁=300(⁰C), p₁=87,6(at), H₁=1345, H_E=2749, S₁=3,255, S_E=5,705; inoltre su quella superiore (2-3): T₂=350(⁰C), p₂=168,6(at); poi (fuori Tabella) T₄=400(⁰C), H₄=2930, S₄=S₅=5,777; quindi la Portata m=10(kg/s), infine (in 5′)calcoliamo (x₅),(H₅) e il Bilancio (2) del Ciclo-HIRN:

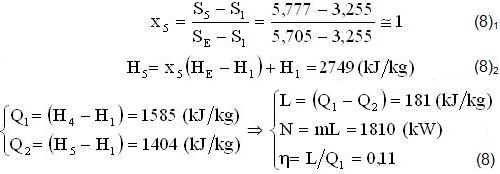
2-A) ENTALPICO DISTILLATORE

(1→1'→1''→2→3→4→5'→6'→6»1),(Tab.A, Tav.2, fig.5,6).

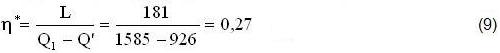
Dal precedente si ottiene il CICLO-ENTALPICO-DISTILLATORE spostando in Basso il nuovo PUNTO-Iniziale (6»1),(T=100°C),(p=1,033at), quindi il RECUPERO di Calore (6’-6) RIDUCE (Q₂=1404) a Q’=(H₁-419)=926, con un RENDIMENTO (η*=0,27) maggiore del 145% rispetto a quello (h=0,11) del CICLO-HIRN di partenza:

Questo Rendimento può diventare UNITARIO (η*=1) Riciclando entrambi i RECUPERI Q*=(Q”+Q’)=(Q₂=1404), Q’=926<(Q₂) e Q”=(1404-926)=478. In tal modo il DISTILLATORE assorbe soltanto quel CALORE necessario a produrre ACQUA-CALDA-Potabile (a 100°C e 1atm) e il LAVORO (L=181) sufficiente a renderlo AUTONOMO:

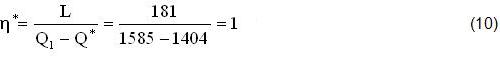
In questi casi occorre perfezionare l’Ottimazione delle 2 Isotermobariche estreme (5′-6′),(2-3) e del Punto-Iniziale (6»1) rispetto al Punto-Critico (C) riducendo al minimo (L→0) il LAVORO L=(4-5′) (Area Racchiusa), eventualmente sostituendo la Turbina (T) con un Riduttore di Pressione. Inoltre (fig.6) conviene utilizzare il Salto di Pressione Δp=(p’-p₁) tramite una TURBINA-IRAULICA (T_O) che convoglia nel Pozzo (Z) il Liquido-Uscente.

RIVENDICAZIONI

I) CICLI-ENTALPICI delle “MACCHINE-TERMICHE-A-VAPORE” definiti in precedenza (Titolo, Descrizione, Tavole e Disegni), di cui Rivendichiamo tutte le possibili VARIANTI e APPLICAZIONI nell’Ambito della RICERCA, tenendo conto delle possibili MODIFICHE, trattandosi di una autentica “NOVITA’-ASSOLUTA”, addirittura incompatibile col “SECONDO-PRINCIPIO-DELLA-TERMODINAMICA”, fondata essenzialmente sulla ERRATA interpretazione del Ciclo-RANKINE-HIRN (fig.1,2), dimostrando che il SUO Primo-LATO (1-2),(dp=0) non si trova (come si CREDE) nella Zona-Liquida (L) ma sulla ISOTITOLO-ISOBARA (x=0),(dp=0) appartenente alla Curva-Limite (AC),(x=0) di (ACBA), con NOTEVOLI ma prevedibili conseguenze TERMODINAMICHE.

II) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.3,5) che i suoi PRIMI-LATI (1-2),(dp=0),(∆T≠0) appartengono alla Curva-Limite (AC),(x=0) di (ACBA), dove l’ENTALPIA del LIQUIDO (H₁) può essere OTTIMIZZATA (H*³H₁)Î(AC) riciclando 2 RECUPERI di CALORE (1-1′),(1-1”),(linee in grassetto) da Alta a Bassa TEMPERATURA, mentre il LAVORO (4-5),(4-5’) (Area-Racchiusa) acquista un RENDIMENTO maggiore del 30-40% rispetto a quello del corrispondente CICLO-RANKINE (fig.1,2).

III) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.5,6),(Tav.2) che nei DISTILLATORI il RENDIMENTO può diventare UNITARIO (h*=1) Riciclando il Calore-Latente di Condensazione Q₂=(5′-6′), tramite i Recuperi (1-1′),(1-1”), OTTIMIZZANDO le posizioni delle ISOTERMOBARICHE estreme (5′-6′),(2-3) e del Punto-Iniziale (6=1), rispetto al Punto-Critico (C).

IV) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.5,6),(Tav.2) che nei DISTILLATORI-SEMPLICI conviene ridurre al minimo il LAVORO (Area-Racchiusa), quasi azzerandolo (L®0), tuttavia quanto BASTA per renderli AUTONOMI, separando il POTABILE (Z) dall’INQUINATO (P_A), favoriti dai RECUPERI (Q”+Q’) ma anche dalla TURBINA-IDRAULICA (T_O),(p’®p₁) che aggiunge LAVORO-UTILE.

V) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.5,6),(Tav.2) che nel DISTILLATORE-SEMPLICE il RENDIMENTO può diventare UNITARIO (h*=1) Riciclando il Calore-Latente di CONDENSAZIONE (1-1′)£(Q₂) oppure entrambi i RECUPERI (1-1′),(1-1”), quando il LAVORO è trascurabile (L®0) e quindi conviene sostituire laTurbina (T) con un Riduttore (R).

VI) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.3,5),(Tav.1,2) che oltre dai RECUPERI-di-CALORE (1-1′),(1-1”)Î(AC),(x=0) il RENDIMENTO può essere Migliorato anche dalle possibili VARIANTI applicate ai moderni IMPIANTI, in particolare dai cosiddetti SPILLAMENTI-di-VAPORE.

VII) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.5,6),(Tav.2) che il più vantaggioso MOTORE-DISTILLATORE, col massimo RENDIMENTO, si ottiene OTTIMIZZANDO le 3 Pressioni (p₁<p'<p₂) affinché si produca il massimo LAVORO (Area -Racchiusa) col massimo RECUPERO (Q*£Q₂).

VIII) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.5,6),(Tav.2) che nel DISTILLATORE-SEMPLICE le due Pressioni (p'<p₂) possono ravvicinarsi fin quasi a coincidere (p’£p₂), in modo tale da ottenere il minimo LAVORO (Area-Racchiusa) col massimo RECUPERO (Q*£Q₂).

IX) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.3,5),(Tav.2) che nel RECUPERO del CALORE-SENSIBILE Q”=(1-1”)Î(x’), comune per tutti i Cicli-Entalpici, conviene impiegare un CIRCUITO-AUTONOMO in parallelo, dove il LIQUIDO-CIRCOLANTE, orientato da un DIREZIOMETRO (N) e agevolato da un POLMONE (M) di GAS-INERTE, viene MOSSO dalla POMPA esterna (P) ad una PRESSIONE costante (p*) abbastanza alta (p*>p₀) rispetto a quella p₀=f(T₀) del VAPORE-SATURO.

X) CICLI-ENTALPICI delle precedenti Rivendicazioni, caratterizzati dal fatto (fig.3,4,5,6) che nella precedente ESPOSIZIONE (Riassunto, Descrizione e Disegni) abbiamo adottato la stessa SIMBOLOGIA dei più comuni MANUALI-TECNICI, omettendo (per brevità) i rispettivi significati scientifici.

Cookie	Durata	Descrizione
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.

(10) MACCHINE TERMICHE A VAPORE Cicli Entalpici, Motori e Distillatori