(12)
CRITERI DI OTTIMAZIONE DEL RENDIMENTO DI UN MOTORE PRIMO TERMICO

Versione integrale del quarto Brevetto, Attestato (link 20)

INTRODUZIONE

Il CALORE è classificato come ENERGIA di SECONDA SPECIE perché può compiere LAVORO CICLICO (ripetibile periodicamente) soltanto tramite MOTORI TERMICI, costituiti essenzialmente da una CAMERA di COMBUSTIONE dove si svolgono i CICLI PRIMARI nel Piano Entropico Ω(T,S) e da un ALBERO MOTORE dove si realizzano i corrispondenti CICLI INDOTTI nel Piano Meccanico O(F,s), TRASFORMANDO (almeno in parte) il CALORE in LAVORO, detto ENERGIA di PRIMA SPECIE.

CAMERA e ALBERO sono collegati da una Trasmissione Meccanica chiamata CATENA CINEMATICA, formata da pochi elementi statici (Condotti, Valvole, Deviatori, ecc.) nelle TURBINE, oppure dal Meccanismo BIELLA-MANOVELLA nei MOTORI ALTERNATIVI.

In questi casi la CATENA CINEMATICA modifica la TERMODINAMICA e il RENDIMENTO dei CICLI TERMICI anche e non solo a causa degli ATTRITI, specialmente nei MOTORI ALTARNATIVI ancor più che nelle TURBINE a GAS di uguale POTENZA.In sostanza le CATENE CINEMATICHE modificano il RENDIMENTO dei MOTORI TERMICI, specie ALTERNATIVI, ma lascia INVARIATO quello dei MOTORI MECCANICI, con valore UNITARIO in assenza di ATTRITI.

Dimostreremo in seguito che MODIFICANDO opportunamente il Meccanismo BIELLA-MANOVELLA si può migliorare il RENDIMENTO dei MOTORI ALTERNATIVI, addirittura fino a SUPERARE quello TEORICO calcolato nella CAMERA di COMBUSTIONE.

Questi RISULTATI (inattesi quanto imprevedibili) mettono in discussione alcuni dei più importanti Teoremi di FISICA SPERIMENTALE, in particolare la VALIDITA' del Postulato di CARNOT-CLAUSIUS, cioè del SECONDO PRINCIPIO della TERMODINAMICA e il suo LEGAME con la FUNZIONE di STATO chiamata ENTROPIA, tenendo conto che anche il RENDIMENTO del CICLO di CARNOT invertibile si svolge in un MOTORE TERMICO e quindi viene condizionato da una CATENA CINEMATICA.

Si tratta dei principali argomenti di una TESI di LAUREA redatta presso "LA SAPIENZA" di ROMA, avente per Titolo:CRITERI di OTTIMAZIONE del RENDIMENTO di un MOTORE PRIMO TERMICO.

Che poi (in Appendice) sconfina in una LEGGE ASSOLUTA (applicabile per via sperimentale) che include la necessaria modifica di altri TEOREMI ritenuti intoccabili, in particolare il Concetto di INTEGRALE INDEFINITO (o PRIMITIVA) di una FUNZIONE CONTINUA.Questi ARGOMENTI formano l'EPILOGO di questa RICERCA.

RIASSUNTO

All’inizio si trattava di CAPIRE perché, a parità di POTENZA,  i MOTORI TERMICI ALTERNATIVI non sono più ECONOMICI delle TURBINE a GAS, pur essendo assai più alti i RENDIMENTI dei CICLI IDEALI, mentre i rispettivi ATTRITI sono quasi IDENTICI.
 
 La DISCORDANZA dipende certamente dalla DIVERSITA’ delle due MACCHINE, cioè dalla CATENA CINEMATICA che collega la CAMERA di COMBUSTIONE all’ALBERO, quasi INESISTENTE nelle TURBINE mentre nei MOTORI ALTERNATIVI è formata dal MECCANISMO BIELLA-MANOVELLA, dove le FORZE TERMICHE del GAS diventano MASSIME nei Punti MORTI, quando la loro utilità è NULLA.
 
 Peraltro, nelle modalità di REGIME (durante il MOTO), ogni MOTORE a Combustione Interna FUNZIONA da SOLO, in modo AUTONOMO, INDIPENDENTE, a SCATOLA CHIUSA, quindi AUTOGESTISCE in TEMPI REALI (Istante per Istante) il suo BILANCIO ENERGETICO, cioè lo SCAMBIO TERMICO (δQ) nella CAMERA di Combustione e MECCANICO (δL) intorno all’ALBERO.
 
 Si intuisce dunque che il RENDIMENTO dei MOTORI TERMICI può essere facilmente migliorato MODIFICANDO adeguatamente i rispettivi MECCANISMI.  
 
 Nei MOTORI ALTERNATIVI (Scoppio, Diesel) ciò si ottiene TRASLANDO l’ALBERO (fig.6,7) a determinata distanza (OH)<(OD) dall’ASSE del CILINDRO, affinché durante il MOTO risulti MASSIMA la FASE di ESPANSIONE ANGOLARE (π+α1)≤φ≤(2π+α2) nel VERSO positivo di rotazione (AOP*). In tal modo il RENDIMENTO può CRESCERE del 20-30%, a volte superando quello TEORICO del CICLO IDEALE:

(π+α1)≤φ≤(2π+α2)    ⇒    (AOP*)

Ma anche la MACCHINA PERFETTA di CARNOT (priva di Attriti) è dotata di MECCANISMI, quindi quelle OTTIMAZIONI possono MODIFICARE il suo RENDIMENTO, cioè l’EQUAZIONE di CLAUSIUS e il DIFFERENZIALE dS=δQ/T chiamato ENTROPIA, che abbiamo RISOLTO nei Piani MECCANICI O(F,s),O(p,V) con EQUAZIONI di STATO Tipo ΔS=f(F,s)=g(p,V), generalmente INDIPENDENTI dallo Scambio TERMICO (δQ), con notevoli ma prevedibili conseguenze FISICO MATEMATICHE, specialmente TERMODINAMICHE.

DESCRIZIONE

 Il RENDIMENTO REALE ηR=LR/QR di qualsiasi MACCHINA TERMICA a Combustione INTERNA dipende certamente dal CICLO IDEALE (ℑ) (Otto, Diesel, Joule, ecc.) OTTENUTO nella CAMERA di COMBUSTIONE, ma anche dagli ATTRITI (λA,λC) che formano il RENDIMENTO INTERNO η0=(1−λA)(1−λC), quello MECCANICO ηA=(1−λA)=LR/L che trasforma LAVORO in CALORE per effetto JOULE (facendo diminuire LR) e quello TERMICO ηC=(1−λC)=Q/QR che disperde CALORE per fughe di Gas e Conduttività Termica (con aumento di QR).
 
 In pratica si Calcola il RENDIMENTO η=L/Q del Ciclo IDEALE (Otto, Diesel, Joule, ecc.) mentre quello REALE ηR=LR/QR si può misurare sull’ALBERO oppure si ricava moltiplicando η=L/Q per η0=ηCηA, un FATTORE CORRETTIVO (η0) che include tutti gli ATTRITI, TERMICI ηC=Q/QR e MECCANICI ηA=LR/L, essendo LR<L<Q<QR:

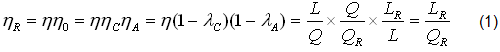
 Per tutti i MOTORI TERMICI le perdite di LAVORO sono in media del 6% con ηA∼0,94 e del 9% quelle di CALORE con ηC∼0,91, come confermano i CICLI INDICATI (ℑ0) dove η0=ηCηA riduce di circa il (6+9)=15% i RENDIMNTI η=L/Q dei CICLI IDEALI. Quindi la (1) può assumere il seguente VALORE STATISTICO approssimato:

Questo RISULTATO (ηR=0,85η) soddisfa mediamente le MACCHINE ROTATIVE, in particolare le TURBINE, ma non le MACCHINE ALTERNATIVE (a Scoppio, Diesel) dove invece si ottiene un VALORE assai INFERIORE, come risulta dal confronto col RENDIMENTO REALE EFFETTIVO (ηR=LR/QR) misurando il LAVORO (LR) intorno all’ALBERO e il CALORE (QR) speso nella CAMERA di Combustione.
   
  Per fare una VERIFICA confrontiamo un MOTORE a SCOPPIO (Otto) con una TURBINA a GAS (Ciclo Joule) di UGUALE POTENZA (fig.1,2), assegnando lo stesso RAPPORTO di COMPRESSIONE, δ=V2/V1=8, β=p2/p1=8, e la COSTANTE Isentropica dell’ARIA k=cp/cv∼1,40, per ottenere i RENDIMENTI (η=L/Q) dei rispettivi CICLI IDEALI:
 Nel Piano O(p,V) uno dei due CICLI inverte le CURVE ISOENTROPICHE rispetto all’altro, (pVk=C)↔(Vpk=C), quindi sono OPPOSTI ma  IDENTICI e compiono lo stesso LAVORO (L∼130 Joule), che DOVREBBE avere lo stesso RENDIMENTO REALE definito dalle (2).
 
 Tuttavia quel risultato ηR∼0,85×0,448∼0,38 è VERO per la TURBINA ma NON per il MOTORE OTTO dove invece al posto di ηR∼0,85×0,565∼0,48 si ottiene all’incirca il valore medio ηR∼(0,48+0,38)/2∼0,43, con un AMMANCO del 24%, (0,43/0,565)∼(1−0,24).
 
 
  Malgrado queste ipotetiche APPROSSIMAZIONI, si SUPPONE che nei MOTORI ALTERNATIVI quel Calo di RENDIMENTO (∼24%) DIPENDE certo dagli ATTRITI λ=λCλA (∼15%) ma soprattutto (in linea col Teorema di CARNOT) dal cosiddetto RENDIMENTO ORGANICO (η0∼9%) della COMBUSTIONE, coinvolgendo (a tale scopo) un insieme di REAZIONI CHIMICHE (poco convincenti) come si usa fare in certi BILANCI ECONOMICI che bisogna far QUADRARE a tutti i costi.
 
 
In effetti non si tiene conto che quella DIMINUZIONE (∼9%) è già INCLUSA nelle Equazioni (2),(3), in quanto tutti i Cicli IDEALI (Otto, Joule, ecc.) IGNORANO la COMBUSTIONE (come se non esistesse). 
 
 
Una conferma emerge dal fatto che nelle TURBINE le FORZE TERMICHE agiscono intorno all’ALBERO, mentre nei MOTORI ALTERNATIVI diventano MASSIME nei PUNTI-MORTI, quando il Meccanismo è ALLINEATO e quindi la loro utilità è NULLA.
 
  Peraltro, nelle normali modalità di REGIME (dopo la messa in moto), ogni MOTORE TERMICO a Combustione Interna AUTOGESTISCE in TEMPI REALI (Istante per Istante) il proprio BILANCIO ENERGETICO, cioè lo Scambio TERMICO (δQ) e MECCANICO (δL) con l’Esterno.
 
 
 In altri termini la MACCHINA funziona da SOLA, in modo AUTONOMO, INDIPENDENTE, a SCATOLA CHIUSA, quindi è certamente il suo MECCANISMO che CREA le CONDIZIONI TERMODINAMICHE del MOTO, compreso il RENDIMENTO. CHI ALTRI SE NO (?).
 
 
  Sostanzialmente, al netto degli ATTRITI (λ=λCλA) e tenendo conto delle correzioni finali (1),(2), possiamo quindi dire che il MECCANISMO produce due Cicli IDEALI CORRISPONDENTI (ℑ)↔(ℑ*), quello PRIMARIO (ℑ) nella CAMERA di COMBUSTIONE e quello INDOTTO (ℑ*) intorno all’ALBERO, come appaiono nelle figure (dal 12 al 19).
 
 
  Possiamo anche dire che, tramite il Meccanismo BIELLA-MANOVELLA, il CICLO PRIMARIO (ℑ) svolto nella CAMERA di COMBUSTIONE produce il Ciclo INDOTTO (ℑ*) intorno all’ALBERO, e viceversa.  
 
 
 
 
 
 
  Nel Piani O(F,s), Ω(T,S), (fig.12,13) questi due CICLI Corrispondenti (ℑ↔ℑ*) hanno la stessa AREA ma differenti FORME GEOMETRICHE, quindi producono lo stesso LAVORO (L=L*) con RENDIMENTI differenti (η∈ℑ)≠(η*∈ℑ*).
 
 
  Ma soltanto il Ciclo INDOTTO (ℑ*) AZIONA l’ALBERO, quindi (idealmente) quel Ciclo potrebbe COLLOCARSI in un ipotetico CILINDRO TOROIDALE intorno all’ALBERO (come nelle TURBINE) IGNORANDO il resto del MOTORE.
 
 
 
 Così facendo lo SCHEMA Termodinamico della MACCHINA verrebbe notevolmente SEMPLIFICATO, tenendo conto che (in ogni caso) nelle (1),(2) dobbiamo SOSTITUIRE il RENDIMENTO INDOTTO (η*∈ℑ*), al posto di quello PRIMARIO (η∈ℑ), per ottenere il seguente RENDIMENTO EFFETTIVO (ηE), valido per ogni MACCHINA TERMICA:
Occorre quindi tracciare (fig.12,13) il 2 CICLI IDEALI CORRISPONDENTI (ℑ↔ℑ*) per conoscere il RENDIMENTO (η*) del CICLO INDOTTO (ℑ*), che poi cercheremo di OTTIMIZZARE fino al Valore MASSIMO (η*)max MODIFICANDO opportunamente la CATENA CINEMATICA, i MECCANISMI che collegano il CILINDRO all’ALBERO.
 
 
 
  In tal modo i RENDIMENTI dei MOTORI ALTERNATIVI possono crescere del 20¸30%, in certi casi superando quelli (η=L/Q) del Ciclo PRIMARIO (ℑ) svolto nel CILINDRO, a differenza delle TURBINE dove nelle EQUAZIONI (2),(4) risulta all’incirca (η∼η*).
 
 
 
 Perciò ci limitiamo a OTTIMIZZARE soltanto il RENDIMENTO dei MOTORI ALTERNATIVI (Scoppio, Diesel), cioè il Meccanismo BIELLA-MANOVELLA ECCENTRICO (fig.6) dove l’ALBERO MOTORE viene TRASLATO alla distanza OTTIMALE h=|OH|≥0 rispetto all’ASSE (PH) del CILINDRO, nel verso positivo di ROTAZIONE φ=(AOP*).
 
 
 
  Per cominciare ricordiamo che lo STATO FISICO di una MASSA M0(kg) di GAS (Ideale, Reale) dipende soltanto (Gibbs) da due VARIABILI. Assegnando la COPPIA (p,V), p=F/A(Pa),V=As(m3), assieme all’altra COPPIA (F,s), F=Ap(N), s=V/A(m), legate dalla COSTANTE AREALE A(m2), tenuto conto delle due COSTANTI FISICHE (R,k), R(J/K), k=cp/cv, allora la TEMPERATURA FISICA RT(J), l’ENTROPIA FISICA Δ(S/R)(adim) e l’ENERGIA INTERNA ΔU(J) assumono le seguenti ESPRESSIONI in Termini Finiti:
  Il Meccanismo BIELLA MANOVELLA (fig.5,6) e le EQUAZIONI (5) consentono di tracciare (fig.12,13) nei Piani O(F,s) Ω(RT,S/R) i due Cicli corrispondenti (ℑ)↔(ℑ*) del MOTORE ALTERNATIVO, quello PRIMARIO (Á) svolto nella CAMERA di COMBUSTIONE (linee tratteggiate) e quello INDOTTO (ℑ*) intorno all’ALBERO (linee intere).
 
Peraltro (fig.3,4) qualsiasi Coppia di Cicli corrispondenti (ℑ↔ℑ*) diventa più esplicita nei PIANI MECCANICI O(F,s) O(F*,s*), dove le due ISENTROPICHE (S/R),(S/R)* creano i 4 PUNTI (X↔X*),(Y↔Y*) di INVERSIONE TERMICA (δQ=0), cioè l’INCREMENTO (Q0) che condiziona il BILANCIO e il RENDIMENTO del Ciclo INDOTTO:

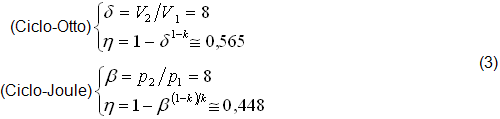
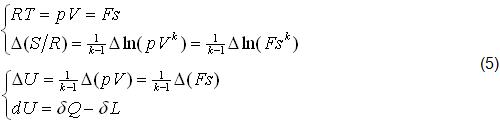
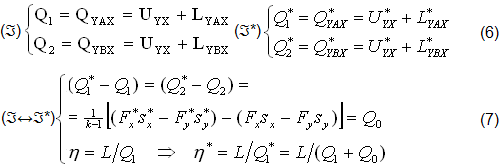
La NOVITA’ delle EQUAZIONI (5),(6),(7) e di altre dello stesso Tipo, che per brevità omettiamo, consiste nel fatto che SEPARANO le grandezze TERMICHE (primi membri) dalle grandezze MECCANICHE (secondi membri).

E’ quanto BASTA per DIMOSTRARE che l’ENTROPIA dS=δQ/T non può rappresentare il TEOREMA di CARNOT, la MISURA della Irreversibilità Termica di CLAUSIUS, una comune FUNZIONE di STATO ΔS=f(p,V)=g(F,s) erroneamente considerata l’ESPRESSIONE MATEMATICA del SECONDO PRINCIPIO DELLA TERMODINAMICA.

A questo punto riteniamo che quanto PRECEDE (Titolo, Riassunto, Descrizione) basti a qualificare le Caratteristiche e lo Scopo della RICERCA, riservandoci (a richiesta) di presentare ulteriori notizie.

Tuttavia, per maggior chiarezza, conviene aggiungere alcuni DETTAGLI corredati da FIGURE, TABELLE, DIAGRAMMI, ESEMPI numerici, che brevemente cercheremo di descrivere tenendo conto di eventuali MODIFICHE e dei possibili ERRORI, omettendo per brevità di commentare i procedimenti che conducono alle EQUAZIONI TERMODINAMICHE (5),(6),(7) e a quelle che seguiranno.

1) CICLI IDEALI.

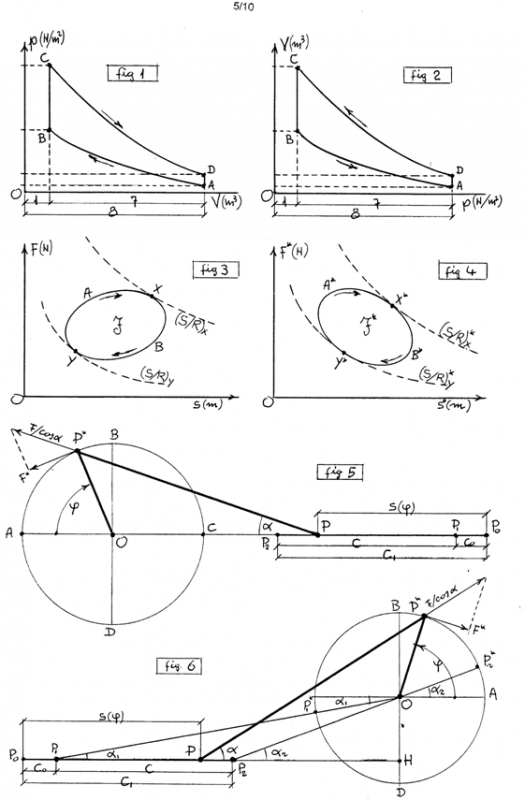
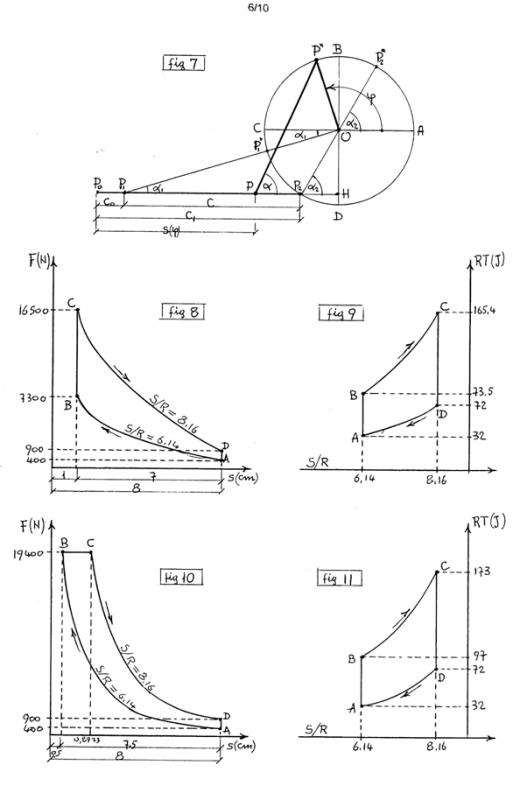
  I Cicli TERMICI si svolgono in un CILINDRO di Sezione A(m2), dove la FORZA F(N) crea la PRESSIONE p=F/A(N/m2) contro lo STANTUFFO che percorre lo SPAZIO s(m) di VOLUME V=sA(m3).
 
 Notevole importanza assumono la TEMPERATURA-FISICA RT(J) e l’ENTROPIA-FISICA S/R(ad.), che dipendono (5) da k=cp/cv(adim.) ma ignorano l’altra COSTANTE R(J/K) e quindi VALGONO per tutti i FLUIDI TERMODINAMICI. Nei nuovi Piani MECCANICO O(F,s) ed ENTROPICO Ω(RT,S/R) le due AREE (δL),(δQ) rappresentano la STESSA quantità di ENERGIA (Joule).

2) MECCANISMO BIELLA-MANOVELLA CENTRATO (fig.5).

 Rappresenta la CATENA CINEMATICA dei MOTORI alternativi, assegnando la BIELLA b=|PP*|, la MANOVELLA r=|OP*|, la CORSA dello STANTUFFO c=2r=|P1P2|, lo SPAZIO NOCIVO c0=|P0P1| e la LUNGHEZZA utile del CILINDRO c1=(c0+c).
 
Il MOTO dipende dall’UNICA VARIABILE j=(AOP*), quando agli ESTREMI (P,P*) di BIELLA (PP*) le FORZE TERMICHE (F,F*) producono (in ogni istante) gli SPOSTAMENTI (ds,ds*).
 
  Le seguenti EQUAZIONI (8) mettono a confronto il LAVORO ELEMENTARE (δL=Fds=F*ds*=δL*=δF*) compiuto dalle FORZE (F,F*) nei PUNTIi (P,P*), che ∀φ≥0 definisce il RAPPORTO di TRASMISSIONE ε(φ) fra le Forze (F*/F) e gli SPOSTAMENTI (ds/ds*):

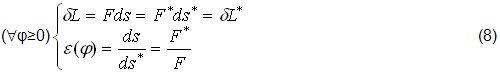
3) MECCANISMO BIELLA-MANOVELLA ECCENTRICO (fig.6,7).

E’ identico al precedente ma l’ALBERO è traslato alla DISTANZA h=|OH≥0 dall’ASSE del CILINDRO. Assegnando
anche l’ESTENSIONE λ=b/r≥2 e l’ECCENTRICITA’ ρ=h/r≥0, le seguenti EQUAZIONI definiscono le INCLINAZIONI  (a1),(a2) della BIELLA, il rapporto CORSA/RAGGIO (c/r), le FASI di COMPRESSIONE (A→B) e di ESPANSIONE (C→D), il MOTO dello STANTUFFO ε(φ)= |P0P|, infine il RAPPORTO di TRASMISSIONE ε(φ):
  Queste EQUAZIONI si ricavano facilmente prestando un po’ di ATTENZIONE alle FIGURE, anche se (assieme alle altre) NON SONO INDISPENSABILI ai fini del Brevetto. Tuttavia, diventano utili nel DIMENSIONAMENTO e nelle OTTIMAZIONI dei MOTORI, specialmente nella compilazione delle TABELLE e nel CONFRONTO deii RENDIMENTI.
 
Per completare la COMPILAZIONE delle TABELLE dei CICLI OTTO e DIESEL nei Piani O(F,s), Ω(RT,S/R), basta conoscere le due ISENTROPICHE estreme (S/R)=cost, equivalenti (5) a (Fsk)=cost, ottenute ASSEGNANDO (fig.8,9) le COORDINATE di due PUNTI, ad esempio quelli, A(F=400N, s=0,08m) e D(F=900N, s=0,08m), che APPLICHEREMO in seguito:
 

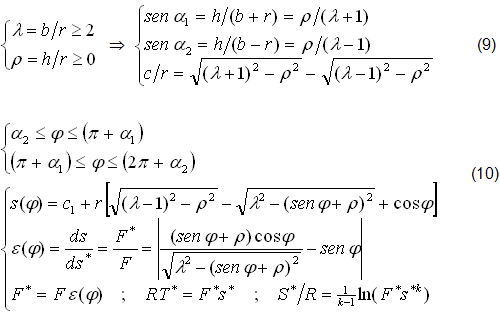
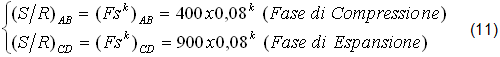
4) OTTIMAZIONE del MECCANISMO ECCENTRICO (fig.6,7).

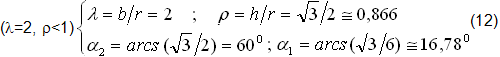
 L’OTTIMAZIONE si ottiene AUMENTANDO per quanto possibile la FASE di ESPANSIONE ANGOLARE (π+α1)≤φ≤(2π+α2)→(AOP*), a scapito della COMPRESSIONE α2≤φ≤(π+α1), cioè col MASSIMO senα2=ρ/(λ-1)<1.
 
 
 
 Per assicurare la CONTINUITA’ del MOTO ∀φ≥0 si assume l’ESTENSIONE λ=b/r e l’ECCENTRICITA’ ρ=h/r negli Intervalli λ=b/r≥2, ρ=h/r<(λ-1), includendo (fig.7) la seguente OTTIMAZIONE limite (λ=2),(ρ=0,866<1):
 
 
 

5) Ciclo IDEALE OTTO, (fig.8,9).

 Questo Ciclo si svolge in un CILINDRO di LUNGHEZZA c1=8cm, SPAZIO NOCIVO c0=1cm, RAPPORTO di COMPRESSIONEd=8/1=8, CORSA dello STANTUFFO c=7cm, FORZA di INIZIO COMPRESSIONE FA=400N e di FINE ESPANSIONE FD=900N, la COSTANTE k»1,40.
 
   Assegnando anche l’ESTENSIONE λ=b/r=4, con le (9),(10),(11) possiamo TRACCIARE (Tabella A),(fig.12,13) il Ciclo OTTO nei Piani O(F,s), Ω(RT,S/R), di cui si conosce l’Isentropica di COMPRESSIONE (S/R)AB∼6,1386, quella di ESPANSIONE (S/R)CD∼8,1659, inoltre le COORDINATE dei 4 VERTICI (A,B,C,D).
 
 
 
 
 Le AREE RACCHIUSE rappresentano ENERGIA (J), cioè il LAVORO nel Piano O(F,s) e il CALORE nel Piano Ω(RT,S/R), misurabili (per una eventuale verifica) nell’unica SCALA: 1(cm2)=10(Joule).
 
 Infine le (5),(6) consentono di calcolare il BILANCIO ENERGETICO del CICLO OTTO, cioè il CALORE ASSORBITO (Q1), il CALORE CEDUTO (Q2) e il LAVORO ESEGUITO L=(Q1-Q2), mentre il RENDIMENTO IDEALE (η=L/Q1) assume lo stesso VALORE (η∼0,565) dell’ESEMPIO (3), come segue:

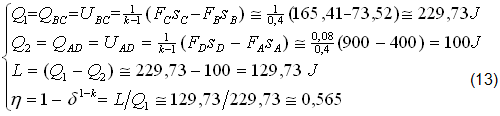
6) CICLO IDEALE DIESEL, (fig.10,11).

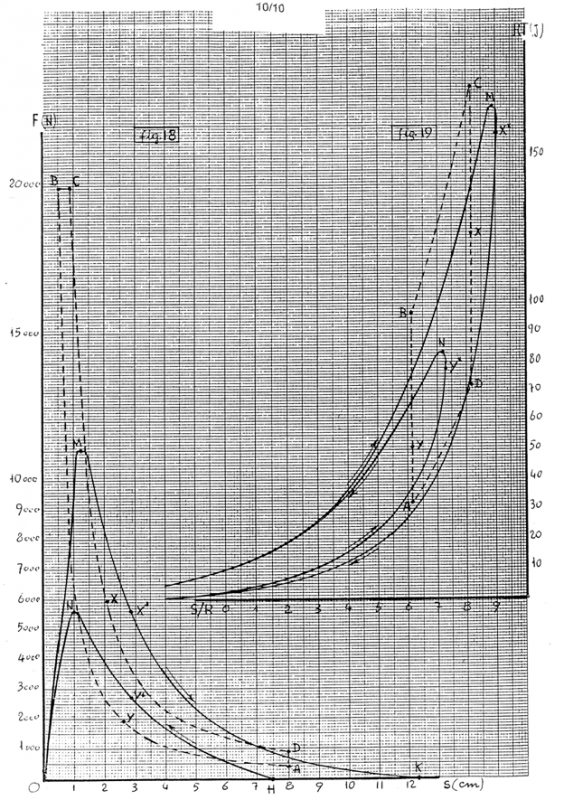
Nei Piani O(F,s) e Ω(RT,S/R), il CICLO si svolge nel precedente CILINDRO, di LUNGHEZZA c1=8cm, SPAZIO NOCIVO c0=sB=0,5cm, RAPPORTO di COMPRESSIONE d=8/0,5=16, CORSA c=7,5cm, ESTENSIONE λ=b/r=4, confermando FA=400N, FD=900N, (S/R)A»6,1386, (S/R)D∼8,1659, con sC∼0,8923, quindi, dopo aver completato i 4 VERTICI (A,B,C,D) si applicano le (6)1 col seguente risultato:

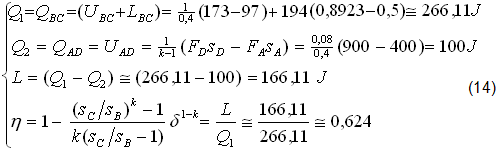
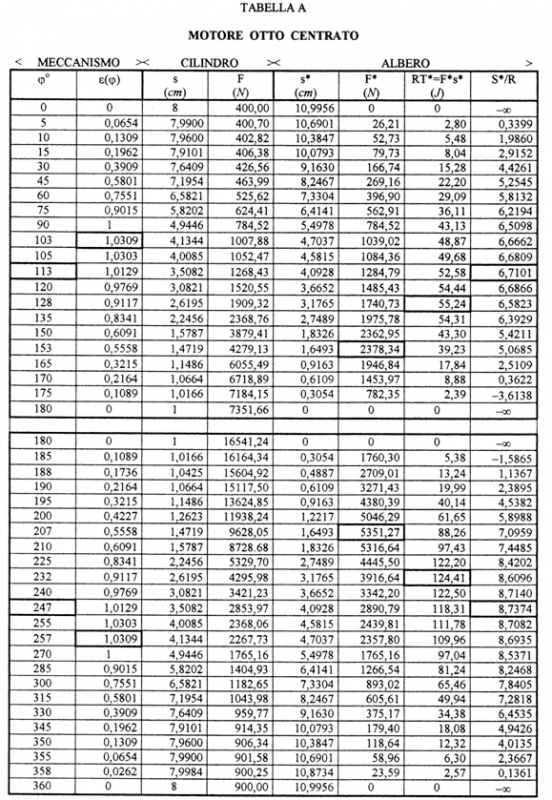
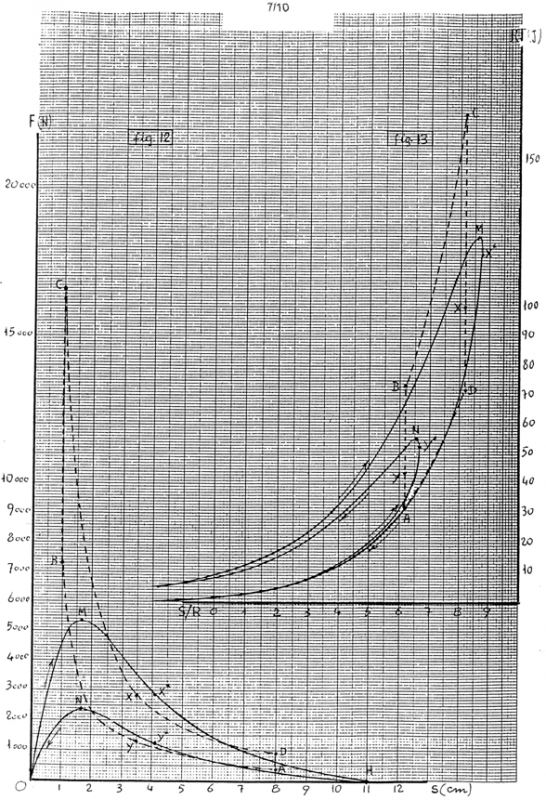
7) MOTORE OTTO CENTRATO (Tabella A e figure 5,12,13).

Il CICLO si svolge nel CILINDRO di LUNGHEZZA utile c1=8.cm, SPAZIO NOCIVO c0=1.cm, COMPRESSIONE d=8/1=8, mentre il MOTORE è azionato dal MECCANISMO CENTRATO (fig.5) ρ=h/r=0, di ESTENSIONE λ=b/r=4 e MANOVELLA r=3,5.cm.

 

 
  Dalle (9),(10) si ricava la il RAPPORTO di TRASMISSIONE ε(φ)=F*/F=ds/ds*, le Fasi di COMPRESSIONE 0≤φ≤π e di ESPANSIONE p≤φ≤2π, inoltre i due CICLI CORRISPONDENTI (ℑ)↔(ℑ*) nei Piani  O(F,s), Ω(RT,S/R), quello PRIMARIO (ℑ) svolto nel CILINDRO (ltratteggiato) e quello INDOTTO (ℑ*) intorno all’ALBERO (linee intere).
Si conferma dunque il CALO (4) ηE∼(0,85×0,509)∼0,43 sul RENDIMENTO ( η*=0,509) del Ciclo INDOTTO:

 Tabella A
jo
e(j)
s(cm)
F(N)
Fs(J)
s*(cm)
F*(N)
F*s*(J)
(S*/R)M
113
1,0129
3,5082
1268,43
 44,50
4,0928
1284,79
 52,58
6,7101
247
1,0129
3,5082
2853,47
100,12
4,0928
2890,79
118,31
8,7374

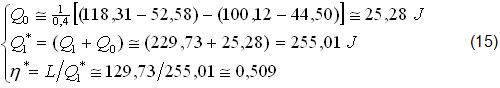
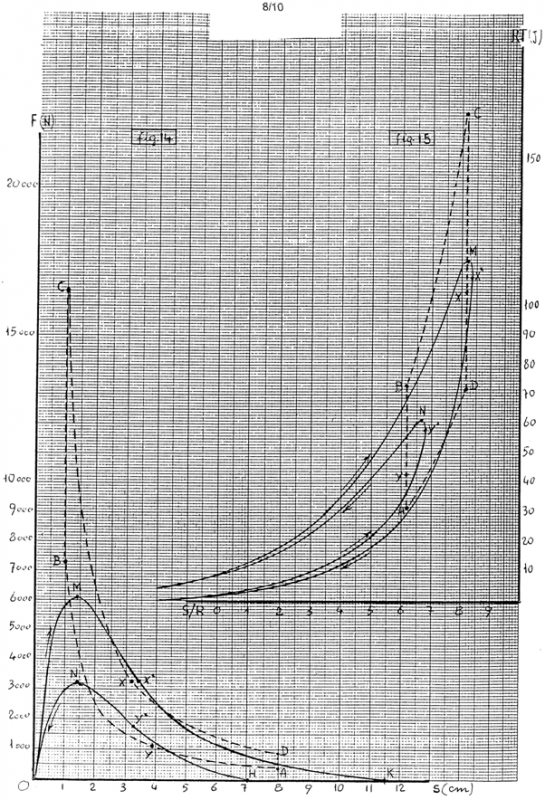
8) MOTORE OTTO ECCENTRICO (Tabella B e figure.7,14,15).

 Al MECCANISMO ECCENTRICO (fig.7) con h=|OH|≥0, si applica l’OTTIMAZIONE (12), cioè l’ESTENSIONE λ=b/r=2 e l’ECCENTRICITA’ ρ=h/r=Ö3/2, nello lo stesso CILINDRO, c0=1cm, c1=8cm, δ=8.
 
 
  Quindi dalle (9),(10) si ricava la nuova MANOVELLA r»2,95.cm, le nuove Fasi di COMPRESSIONE 600≤φ≤1970 e di ESPANSIONE 1970≤φ≤4200, ottenendo infine i due CICLI CORRISPONDENTI (ℑ)↔(ℑ*) nei Piani Meccanico O(F,s) ed Entropico Ω(RT,S/R), sempre nell’unica SCALA: 1cm2=10.Joule.
 
 
 
 In questo caso i 4 PUNTI (X↔Y),(X*↔Y*) di massima ENTROPIA si trovano nelle due RIGHE (φ=1330),(φ=2620) della TABELLA B, dove le EQUAZIONI (6),(7) definiscono l’INCREMENTO TERMICO Q0 e il RENDIMENTO (η*=0,634) del nuovo CICLO INDOTTO OTTIMIZZATO (ℑ*), che deve SOSTITUIRE quello (η*=0,509) OTTENUTO con le (15):

jo
e(j)
s(cm)
F(N)
Fs(J)
s*(cm)
F*(N)
F*s*(J)
(S*/R)M
133
1,6366
3,9118
1089,08
 42,60
3,2846
1782,39
 58,54
6,7585
262
0,9989
3,1746
3282,49
104,21
3,3589
3278,88
110,13
8,3607

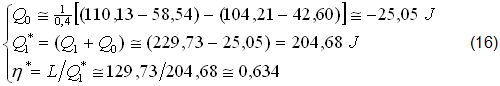
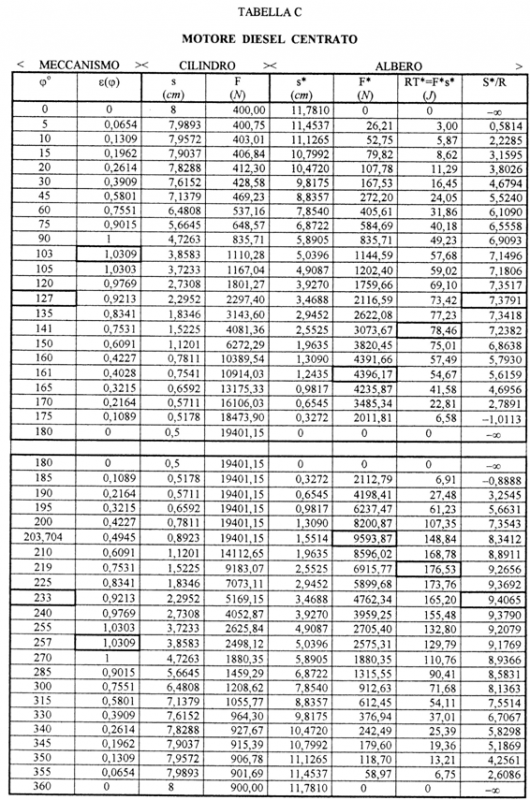
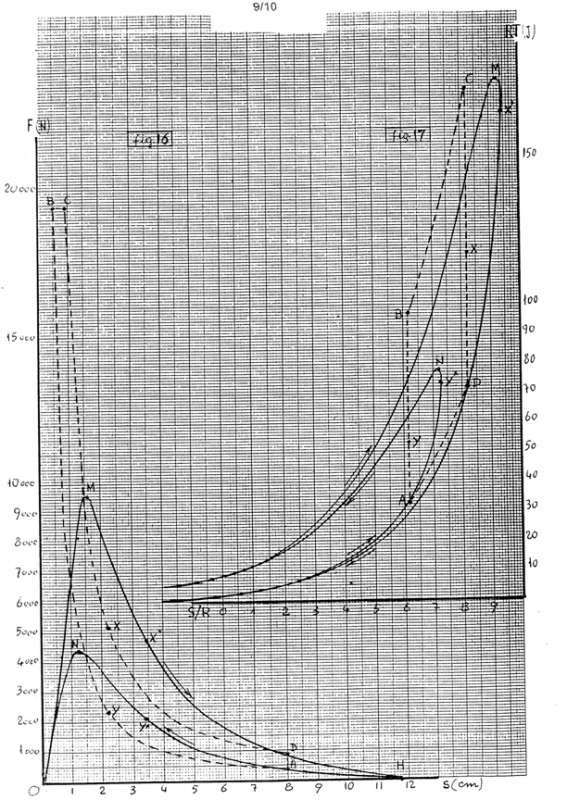
9) MOTORE DIESEL CENTRATO (Tabella C e figure 5,16,17).

Il MECCANISMO di Estensione λ=b/r=4, e il CILINDRO di Lunghezza c1=8.cm, sono gli stessi del MOTORE OTTO, dove però si assegna lo SPAZIO NOCIVO c0=0,5.cm, il RAPPORTO di Compressione d=8/0,5=16 e la nuova MANOVELLA r=7,5/2=3,75.cm. 
 
Per il resto le (9),(10) definiscono i due CICLI Corrispondenti (ℑ)↔(ℑ*) nei Piani O(F,s), Ω(RT,S/R), quello PRIMARIO (ℑ) svolto nel CILINDRO (linee tratteggiate) e quello INDOTTO (ℑ*) intorno all’ALBERO (linee intere), nella Scala: 1.cm2=10.Joule.
 
In questo caso nelle due righe (φ=1270),(φ=2330) della TABELLA C convergono i QUATTRO PUNTI (X↔Y),(X*↔Y*) di Massima ENTROPIA, che definiscono l’Incremento TERMICO Q0 e quindi anche il BILANCIO ENERGETICO (6),(7) del nuovo CICLO DIESEL INDOTTO (ℑ*) assieme al suo RENDIMENTO (η*):

 Tabella C
jo
e(j)
s(cm)
F(N)
Fs(J)
s*(cm)
F*(N)
F*s*(J)
(S*/R)M
127
0,9213
2,2952
2297,40
 52,73
3,4688
2116,59
 73,42
7,3791
233
0,9213
2,2952
5169,15
118,64
3,4688
4762,34
165,20
9,4065

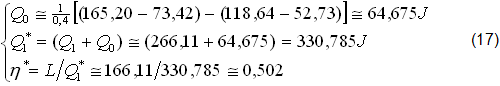
Il Rendimento INDOTTO (η*∼502) risulta inferiore del 20% rispetto a (14),(η∼0,624) del CICLO PRIMARIO. Anche adesso l’APPROSSIMAZIONE (4) ηE∼0,85x0,502∼0,43 diventa affidabile IGNORANDO la COMBUSTIONE.

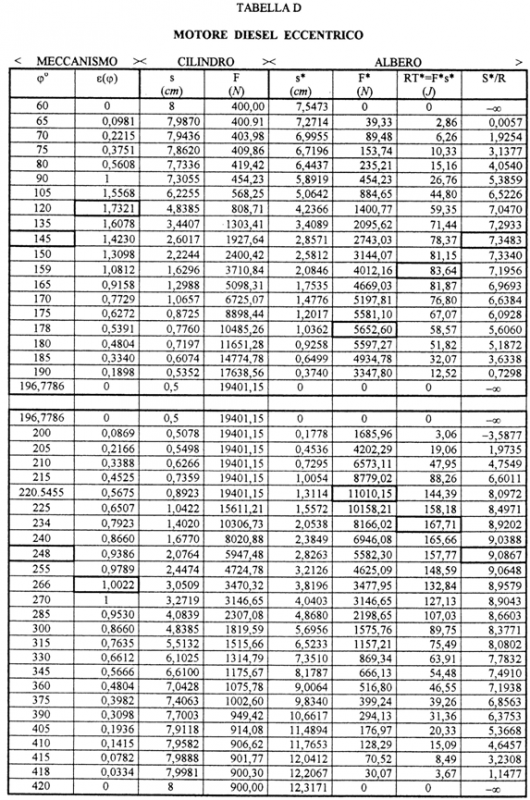
10) MOTORE DIESEL ECCENTRICO (Tabella D e figure 10,11).

 Al precedente MOTORE Centrato (14) applichiamo l’OTTIMAZIONE (12), cioè l’ESTENSIONE λ=b/r=2 e l’ECCENTRICITA’ ρ=h/r=Ö3/2
 
Tramite le (9),(10) calcoliamo quindi la nuova MANOVELLA r∼2,95.cm, le Fasi di COMPRESSIONE 600≤φ≤1970 e di ESPANSIONE 1970≤φ≤4200, inoltre i due CICLI Corrispondenti (ℑ)↔(ℑ*), anch’essi tabellati e disegnati nei PIANI O(F,s), Ω(RT,S/R).
 
 Anche in questo caso conviene EVIDENZIARE i 4 PUNTI (X,X*),(Y,Y*) di massima ENTROPIA (S*/R)M le cui COORDINATE si trovano nelle due righe (φ=1450),(φ=2480) della TABELLA D, dove le EQUAZIONI (6),(7) consentono di calcolare l’INCREMENTO TERMICO Q0 (da ℑ a ℑ*) e quindi il RENDIMENTO (η*) del CICLO DIESEL INDOTTO (ℑ*) agente intorno all’ALBERO, che quanto prima SOSTITUISCE quello (h=0,624) del CICLO PRIMARIO (ℑ) svolto nel CILINDRO:

 Tabella D
jo
e(j)
s(cm)
F(N)
Fs(J)
s*(cm)
F*(N)
F*s*(J)
(S*/R)M
145
1,4230
2,6017
1927,64
 50,15
2,8571
2743,03
 78,37
7.3483
248
0,9386
2,0764
5947,48
123,49
2,8263
5582,30
157,77
9,0867

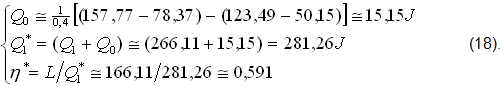
Questo RENDIMENTO INDOTTO (η*∼0,591) è inferiore del 5% rispetto a quello (14),(η∼0,624) del CICLO PRIMARIO (ℑ) svolto nel CILINDRO, ma supera del 18% il RENDIMENTO INDOTTO (17),(η*∼0,502) del MOTORE DIESEL CENTRATO.

11) CONCLUSIONE

Il RENDIMENTO di tutte le MACCHINE TERMICHE a Combustione Interna può CRESCERE notevolmente OTTIMIZZANDO le CATENE CINEMATICHE, cioè MODIFICANDO opportunamente i rispettivi MECCANISMI che trasmettono le FORZE Termiche del Gas dalla CAMERA di Combustione all’ALBERO.

RIVENDICAZIONI

1) OTTIMAZIONE DEI MOTORI-TERMICI definita in precedenza (Titolo, Riassunto, Descrizione, Disegni), di cui RIVENDICHIAMO tutte le APPLICAZIONI e MODIFICHE, trattandosi di una NOVITA’ incompatibile col SECONDO-PRINCIPIO-della-TERMODINAMICA.
2) OTTIMAZIONE DEI MOTORI-TERMICI come nella precedente RIVENDICAZIONE,caratterizzati dal fatto che nelle modalità di REGIME (dopo la messa in MOTO), ogni MOTORE-TERMICO a Combustione-Interna FUNZIONA, in modo AUTONOMO, INDIPENDENTE, a “SCATOLA-CHIUSA”, quindi AUTOGESTISCE in TEMPI-REALI (istante per istante) il suo BILANCIO-ENERGETICO, cioè lo SCAMBIO TERMICO (dQ) e MECCANICO (dL) con l’ESTERNO, AUTOGESTENDO anche il suo RENDIMENTO.
3) OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto che i MOTORI-ALTERNATIVI non sono più economici delle TURBINE di uguale POTENZA, pur essendo più alti i RENDIMENTI dei CICLI-IDEALI, mentre gli ATTRITI sono quasi IDENTICI.  La DISCORDANZA dipende dalla diversità delle due MACCHINE, dato che nelle TURBINE le FORZE agiscono sull’ALBERO mentre nei MOTORI-ALTERNATIVI diventano Massime nei Punti-Morti, dove la l’utilità è NULLA.
4) OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto che il RENDIMENTO delle MACCHINE-TERMICHE può CRESCERE notevolmente OTTIMIZZANDO le loro CATENE-CINEMATICHE, cioè MODIFICANDO opportunamente i MECCANISMI che trasmettono le FORZE-TERMICHE del GAS dalla CAMERA di COMBUSTIONE all’ALBERO.
5) OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto che nelle TURBINE un miglioramento del RENDIMENTO si può ottenere MODIFICANDO opportunamente le PALE delle GIRANTI affinché le FORZE-MOTRICI agiscano il più possibile TANGENTI all’ALBERO.
6) OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto che tutti i MOTORI-ALTERNATIVI sono azionati dal MECCANISMO-BIELLA-MANOVELLA, dove Forze Termiche diventano massime nei PUNTI-MORTI-Superiori, quando la loro utilità è NULLA. Quindi presenta molto interesse l’OTTIMAZIONE dei rispettivi RENDIMENTI, che possono CRESCERE anche oltre il 30%.
7) OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto che l’OTTIMAZIONE dei MOTORI-ALTERNATIVI si ottiene (fig.6) decentrando l’ALBERO alla massima distanza h=|OH| dall’ASSE del CILINDRO, dopo avere IMPOSTO il verso positivo di ROTAZIONE concorde alla nuova FASE di ESPANSIONE (p+a1)£j£(2p+a2).
8) OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto (fig.6) che per assicurare la CONTINUITA’ del MOTO “φ≥0 conviene assegnare l’ESTENSIONE λ=b/r e l’ECCENTRICITA’ r=h/r negli Intervalli (λ≥2),[r<(λ−1)], che escludono i PUNTI-SINGOLARI (λ<2),(r≥1).
9) OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto (fig.7) che, escludendo i PUNTI-SINGOLARI (λ<2),(r≥1), il MASSIMO-RENDIMENTO si ottiene (10) assegnando la MASSIMA-ESPANSIONE (a1+p)£j£(2p+a2) e la MINIMA-COMPRESSIONE a2£j£(p+a1), cioè il massimo valore di sena2=r/(l-1)<1 nell’intervallo 0<r<(l-1)<1. L’OTTIMAZIONE-LIMITE (12), con l=b/r=2 e r=~0.866(<1), SODDISFA a queste CONDIZIONI, già applicata a titolo di ESEMPIO, ottenendo fra l’altro un MOTORE-OTTO-ECCENTRICO dove il RENDIMENTO-Indotto (h*»0,634) supera del 20% quello (h*»0,509) del CICLO-Primario svolto nel CILINDRO e del 32% quello (h=0,43) del corrispondente MOTORE-CENTRATO.
10)  OTTIMAZIONE DEI MOTORI-TERMICI come nelle precedenti RIVENDICAZIONI, caratterizzata dal fatto che nei MOTORI-ECCENTRICI (h=|OH|>0) si possono RIDURRE le VIBRAZIONI accoppiando due o più CILINDRI-Coassiali in PARALLELO con FASI contrapposte, a parte eventuali VOLANI. Si riducono inoltre gli ATTRITI prodotti dall’ECCENTRICITA’ r<(l-1),”l³2, collegando l’Asta-del-Pistone al MECCANISMO tramite TESTA-CROCE, come AVVIENE in alcune MACCHINE a VAPORE.

Seguono i DISEGNI (4 Tabelle e 19 Figure).