(13)
CICLOIDE ELLITTICA

impiegata nella TURBO-POMPA (primo Brevetto)

DESCRIZIONE

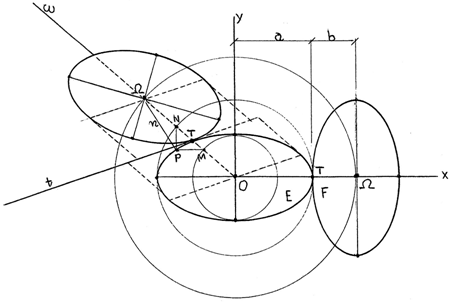
Nel Piano Cartesiano Ortogonale O(x,y) consideriamo le 2 ELLISSI UGUALI (E=F) inizialmente in posizione CANONICA (fig.1), di SEMIDIAMETRI (a≥b>0) e CENTRI (O,Ω) sull’orizzontale (O,x), posti alla distanza |OΩ|=a+b, dove si trova anche il PUNTO di TANGENZA (T) legato al segmento (O,Ω) dall’Equazione:

|OT|+|TΩ|=|OΩ|=a+b

Si intuisce che questa EQUAZIONE potrebbe estendersi al ROTOLAMENTO di (F) intorno a (E) o Viceversa, sapendo che questo accade certamente nelle 4 POSIZIONI CANONICHE di (E=F), quando il RAGGIO POLARE (O,ω) assume le corrispondenti COORDINATE ANGOLARI (0),(π/2),(2π/2),(3π/2) rispetto all’ASSE (O,x).

Per iniziare tracciamo le tre CIRCONFERENZE di CENTRO (O) e RAGGI (b),(a),(a+b), che intersecano la SEMIRETTA (O,ω) in (Ω) e nei PUNTI (M,N), dai quali si ricava il generico PUNTO P∈(E), cioè la COSTRUZIONE (per Punti) dell’ELLISSE (E).

Inoltre (come noto) la NORMALE (P,n) a (E) in P∈(E) interseca la SEMIRETTA (O,ω) nel Punto (Ω), sulla CIRCONFERENZA di RAGGIO (a+b). Analogamente, le 3 CIRCONFERENZE di CENTRO (Ω) e RAGGI (b),(a),(a+b) consentono la COSTRUZIONE per PUNTI dell’altra ELLISSE (F') e del CENTRO (O) di (E).

In tal modo si ottengono le due ELLISSI UGUALI (E=F'), di SEMIDIAMETRI (a,b) e CENTRI (O,Ω), situati sulla SEMIRETTA (O,ω) alla DISTANZA |OΩ|, le quali risultano TANGENTI nel PUNTO di CONTATTO T∈(O,ω).

Per fare una VERIFICA (non necessaria) si può dimostrare che durante il ROTOLAMENTO di (F=F’) intorno a (E), i due SEMIDIAMETRI r1=|OT|∈(E) e r2=|TΩ|∈(F’), CONIUGATI con la TANGENTE (T,t), definiscono le EQUAZIONI CANONICHE di (E=F’) nei rispettivi Piani O(X,Y) e Ω(X,Y), di cui la SEMIRETTA (O,ω) contiene uno dei due ASSIi (X,Y), TRASLATI e OBLIQUI nel Piano Ortogonale O(x,y):
 
 

Di conseguenza, le 2 ELLISSI UGUALI (E=F) di SEMIASSI (a≥b>0) e CENTRI (O,Ω), supposti FISSI alla DISTANZA |OΩ|=(a+b), possono ROTOLARE l’UNA sull’ALTRA (nei versi opposti) SENZA STRISCIARE mantenendo il mutuo CONTATTO TANGENZIALE (T), che diventa il CENTRO ISTANTANEO di ROTAZIONE, in MOTO Rettilineo Alternato nell’INTERVALLO b≤|OT|≤a del SEGMENTO (O,Ω), mentre la TANGENTE (T,t) risulta variamente INCLINATA rispetto alla SEMIRETTA (O,Ω).

Dato l’arbitrario ORIENTAMENTO della SEMIRETTA (O,ω), possiamo dire che la CIRCONFERENZA di CENTRO (O) e RAGGIO |OΩ|=(a+b) rappresenta la CICLOIDE ELLITTICA, che abbiamo definito:

il LUOGO dei PUNTI DESCRITTI dal CENTRO (Ω) durante il ROTOLAMENTO di (F) INTORNO a (E) o VICEVERSA

Questo TEOREMA consente importanti APPLICAZIONI CIVILI e INDUSTRIALI, malgrado l’inevitabile VIBRAZIONE che però può essere notevolmente RIDOTTA applicando due o più COPPIE ELLITTICHE in SERIE nelle rispettive POSIZIONI CANONICHE, VINCOLATE e ugualmente SFASATE sullo stesso ALBERO MOTORE di ASSE (O).